Trilinos::Sacado example documentation

Example usage of Sacado for tensor calculus

Author

jfriedlein

Introduction

The way we see and use Sacado here is as follows:
If you usually compute the following equation

\[ c = a + b \]

for instance with data types double as

\[ 1.0 + 1.0 \rightarrow 2.0 \]

your results is just a double number \( c \) that contains the value \( 2 \).
Using Sacado, on the other hand, the variable \( c_{fad} \) is now of, for example, data type

Sacado::Fad::DFad<double> c_fad;

As a result, \( c_{fad} \) now contains not just the number \( 2 \), but also all the derivatives of \( c_{fad} \) with respect to the previously defined degrees of freedom (set via command *.diff(*)).
The following figure tries to visualize this for first derivatives:

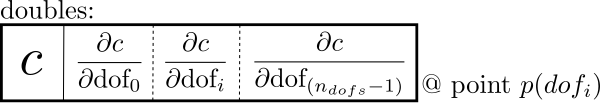
and for second derivatives (requires different data type):

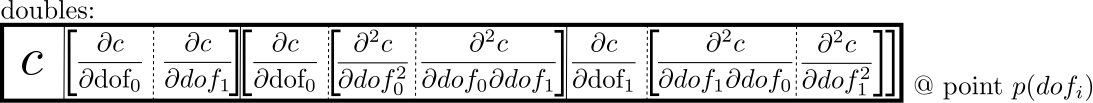
Every variable that was declared as such a data type now contains besides the actual value \( c \), also its derivatives.

Overview

Todo:

Add the example 10 (templated functions) to the overview and some text on why to use it

add the example 9 (factor 0.5) to the background group

This overview shall give you a first impression what to expect from each of the examples. The background/basics group gives you the promised look under the hood. Whereas the application group shows you how you can use the Sacado_Wrapper to quickly compute tangents.

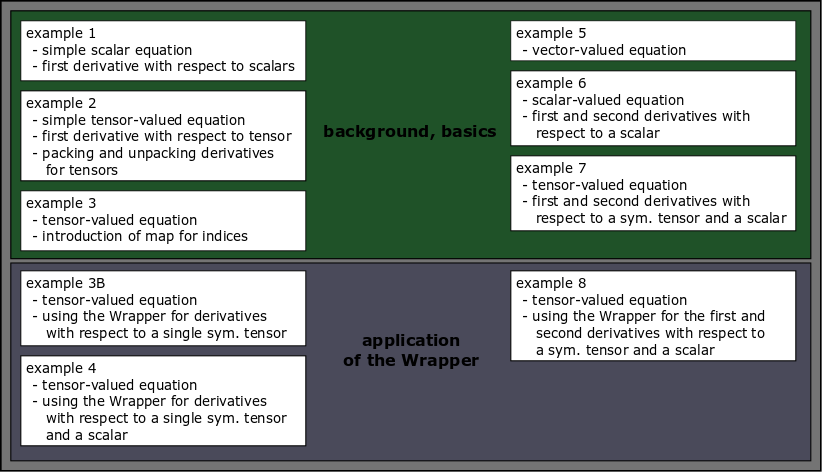
If you right away want to use Sacado, then you might skip the first examples and jump to example 3B. There we show how to use the "Sacado_Wrapper" that does everything from example 2 and example 3 in just a view lines of code. This does not mean that the here shown approach is the fastest or most efficient, it is just simple and easy to use.

Furthermore, if you, for instance, compute problems with two-fields (e.g. displacement and scalar damage) and you need tangents with respect to both a tensor (e.g. strain tensor) and a scalar (e.g. damage variable), you can use the Sacado_Wrapper as shown in example 4.

Some more basics

One can access the double value of \( c_{fad} \) with the Sacado command *.val():

double c_value = c_fad.val();

The derivatives of \( c_{fad} \) can be accessed with the command *.dx():

double d_c_d_a = c_fad.dx(0);
double c_c_d_b = c_fad.dx(1);

The arguments of dx, namely 0 and 1 are the numbers corresponding to the dof that belong to a and b. More details on how to set this up and use it, are given in example 1.

Some resources/links

You can use Sacado to compute general derivatives of functions (with or without tensors) with respect to variables (double, Tensors, ...).

Todo:

Link is broken

• Basics on Sacado, automatic differentation and coding examples (important remarks, e.g. on point of non-differentiability):
  https://software.sandia.gov/SESS/past_seminars/111307_Phipps.pdf
• Basics and available autodiff libraries provided by deal.ii:
  https://www.dealii.org/current/doxygen/deal.II/group__auto__symb__diff.html
• Template-based generic programming:
  downloads.hindawi.com/journals/sp/2012/202071.pdf
• Tutorial 33 by deal.ii: introduction to Sacado and implementation to assemble the residuum and compute its derivative
  https://www.dealii.org/current/doxygen/deal.II/step_33.html

The here shown examples shall solely show how Sacado can be applied and give some background and a look under the hood. The code is neither elegant nor efficient, but it works. A more user-friendly version is provided by means of the "Sacado_Wrapper".

Todo:

Check if factor 0.5 is also necessary for d_sigma / d_phi

Note

This documentation and code only protocol my first steps with Sacado. They are not guaranteed to be correct neither are they verified. Any comments, criticism, corrections, feedback, improvements, ... are appreciated and very well welcomed.

The commented program

/*
 * Author: jfriedlein, 2019
 *      dsoldner, 2019
 */

Include Files

The data type SymmetricTensor and some related operations, such as trace, symmetrize, deviator, ... for tensor calculus

#include <deal.II/base/symmetric_tensor.h>

C++ headers (some basics, standard stuff)

#include <iostream>
#include <fstream>
#include <cmath>

TimerOutput: to measure the time spent in certain parts of the code

#include <deal.II/base/timer.h>

Sacado (from Trilinos, data types, operations, ...)

#include <Sacado.hpp>
 
#include "Sacado_Wrapper.h"
#include "Sacado-auxiliary_functions.h"

Those headers are related to data types and autodiff, but don't seem to be needed (nor make a difference)

//#  include <deal.II/base/numbers.h>
//#  include <deal.II/differentiation/ad/ad_number_traits.h>
//#  include <deal.II/differentiation/ad/sacado_number_types.h>

According to the basics of deal.ii-programming (see dealii.org and https://www.dealii.org/current/doxygen/deal.II/step_1.html for a start)

using namespace dealii;

Defining a data type for the Sacado variables (here we simply used the standard types from the deal.ii step-33 tutorial's introduction)

using fad_double = Sacado::Fad::DFad<double>;   // this data type now represents a double, but also contains the derivative of this variable with respect to the defined dofs (set via command *.diff(*))

1. example: simple scalar equation

1. example: simple scalar equation from deal.ii-tutorial step-33 (see the introduction there to get a first impression, https://www.dealii.org/current/doxygen/deal.II/step_33.html)

   Todo:

   clean up the documentation of the classes

   //
   void sacado_test_scalar ()
   {
       std::cout << "Scalar Test:" << std::endl;

   Define the variables used in the computation (inputs/independent variables: a, b; output/result: c; auxiliaries/passive variables: *) as the Sacado-data type

   fad_double a,b,c;

   Initialize the input variables a and b; This (a,b) = (1,2) will be the point where the derivatives are computed. Compare: y=x² -> (dy/dx)(@x=1) = 2. We can only compute the derivative numerically at a certain point.

    a = 1;
    b = 2;
   
   a.diff(0,2);  // Set a to be dof 0, in a 2-dof system.
   b.diff(1,2);  // Set b to be dof 1, in a 2-dof system.

   Our equation here is very simply. But you can use nested equations and many standard mathematical operations, such as sqrt, pow, sin, ...

   c = 2*a + std::cos(a*b);
   double *derivs = &c.fastAccessDx(0); // Access the derivatives of

   Output the derivatives of c with respect to the two above defined degrees of freedom (dof)

       std::cout << "Derivatives at the point (" << a << "," << b << ")" << std::endl;
       std::cout << "dc/da = " << derivs[0] << ", dc/db=" << derivs[1] << std::endl;
   }

2. example: Preparation for the use of Sacado with tensors

Here we want to introduce tensors for the first time. Hence, we limit ourselves to a trivial equation relating the strain tensor eps with dim x dim components with the stress tensor sigma. Both here used tensors are symmetric, hence we use the SymmetricTensor class and have to keep some details in mind (see below factor 0.5 related to Voigt-Notation). Don't be scared by the enormous number of repetitive lines of code, everything shown in this example and the following will be handled by the Sacado_Wrapper with roughly four lines of code.

/*
 * 2. example: use of tensors
 */
void sacado_test_2 ()
{
    std::cout << "Test 2:" << std::endl;

First we set the dimension dim: 2D->dim=2; 3D->dim=3
This defines the "size" of the tensors and the number of dofs. Example 2 only works in 3D, whereas the following Ex3 is set up dimension-independent.

const unsigned int dim = 3;

Declare our input, auxiliary and output variables as SymmetricTensors consisting of fad_doubles (instead of the standard SymmetricTensor out of doubles)

SymmetricTensor<2,dim, fad_double> sigma, eps;

Init the strain tensor (the point at which the derivative shall be computed)

eps[0][0] = 1;
eps[1][1] = 2;
eps[2][2] = 3;
eps[0][1] = 4;
eps[0][2] = 5;
eps[1][2] = 6;

Now we declare the dofs. The derivative to a tensor requires all components, therefore we set the components of the strain tensor here one by one as the dofs. Because our tensors are symmetric, we only need 6 components in 3D instead of 9 for a full second order tensor

eps[0][0].diff(0,6);
eps[1][1].diff(1,6);
eps[2][2].diff(2,6);
eps[0][1].diff(3,6);
eps[0][2].diff(4,6);
eps[1][2].diff(5,6);

The equation describing the stresses (here just a simple test case)

sigma = eps;

Let's output the computed stress tensor.

std::cout << sigma << std::endl;

The resulting values of sigma are fairly boring, due to our simple equation. It is the additional output generated by this, that is interesting here:
output:
1 [ 1 0 0 0 0 0 ] 4 [ 0 0 0 1 0 0 ] 5 [ 0 0 0 0 1 0 ] 4 [ 0 0 0 1 0 0 ] 2 [ 0 1 0 0 0 0 ] 6 [ 0 0 0 0 0 1 ] 5 [ 0 0 0 0 1 0 ] 6 [ 0 0 0 0 0 1 ] 3 [ 0 0 1 0 0 0 ]
The numbers 1, 4, 5, 4, ... are the entries in the stress tensor sigma. In square brackets we see the derivatives of sigma with respect to all the dofs set previously given in the order we defined them above. Meaning: The first entry in the square brackets corresponds to the 0-th dof set by

eps[0][0].diff(0,6); 

referring to the component (0,0) in the strain tensor eps.

Computing the derivatives for certain components of the resulting tangent modulus:
We now access these lists of derivatives (output above in square brackets) for one component of the stress tensor sigma at a time.

{

Access the derivatives corresponding to the component (0,0) of the stress tensor sigma

double *derivs = &sigma[0][0].fastAccessDx(0);

The following output will show us the same derivatives that we already saw above, just formatted differently
output: d_sigma[0][0]/d_eps = 1 , 0 , 0 , 0 , 0 , 0 ,

    std::cout << "d_sigma[0][0]/d_eps = ";
    for ( unsigned int i=0; i<6; ++i)
        std::cout << derivs[i] << " , ";
    std::cout << std::endl;
}
{

Access the derivatives corresponding to the component (1,2) of the stress tensor sigma

double *derivs = &sigma[1][2].fastAccessDx(0);

output: d_sigma[1][2]/d_eps = 0 , 0 , 0 , 0 , 0 , 1 ,

        std::cout << "d_sigma[1][2]/d_eps = ";
        for ( unsigned int i=0; i<6; ++i)
            std::cout << derivs[i] << " , ";
        std::cout << std::endl;
    }
}

3. example: Using a slightly more complicated stress equation

void sacado_test_3 ()
{
    std::cout << "Test 3:" << std::endl;
 
    const unsigned int dim = 3;

Here we also define some constant, for instance the bulk modulus kappa and the second Lamè parameter mu. We now also define one of our constants as fad_double. By doing this we can use the normal multiplication (see below).

double kappa_param = 5;
fad_double kappa (kappa_param);

The second constant remains as a double just to show the difference.

double mu = 2;

SymmetricTensor<2,dim, fad_double> sigma, eps;

To simplify the access to the dofs we define a map that relate the components of our strain tensor to the dof-nbr

std::map<unsigned int,std::pair<unsigned int,unsigned int>> std_map_indicies;

The point at which the derivative shall be computed:
As mentioned previously, we will implement this example for 2D and 3D, hence we once have to set up a strain tensor and the derivatives for 3D with 6 independent components ...

if(dim==3)
{
    eps[0][0] = 1;
    eps[1][1] = 2;
    eps[2][2] = 3;

    eps[0][1] = 4;
    eps[0][2] = 5;
    eps[1][2] = 6;


    eps[0][0].diff(0,6);
    eps[0][1].diff(1,6);
    eps[0][2].diff(2,6);
    eps[1][1].diff(3,6);
    eps[1][2].diff(4,6);
    eps[2][2].diff(5,6);

By using the map and the following pairs, we have to set up the relation between strain components and dofs only once and can use the map to access the entries of the list later, without possibly mixing up indices and creating errors. Please don't be confused, but the dofs in the Wrapper are set up in a different order that we showed earlier. Earlier: (0,0)-(1,1)-(2,2)-...; Now: (0,0)-(0,1)-(0,2)-...

    std::pair<unsigned int, unsigned int> tmp_pair;
    tmp_pair.first=0; tmp_pair.second=0;
    std_map_indicies[0] = tmp_pair;

    tmp_pair.first=0; tmp_pair.second=1;
    std_map_indicies[1] = tmp_pair;

    tmp_pair.first=0; tmp_pair.second=2;
    std_map_indicies[2] = tmp_pair;

    tmp_pair.first=1; tmp_pair.second=1;
    std_map_indicies[3] = tmp_pair;

    tmp_pair.first=1; tmp_pair.second=2;
    std_map_indicies[4] = tmp_pair;

    tmp_pair.first=2; tmp_pair.second=2;
    std_map_indicies[5] = tmp_pair;
}

... and once for 2D with just 3 independent components.

else if(dim==2)
{
    eps[0][0] = 1;
    eps[1][1] = 2;

    eps[0][1] = 4;


    eps[0][0].diff(0,3);
    eps[0][1].diff(1,3);
    eps[1][1].diff(2,3);

    std::pair<unsigned int, unsigned int> tmp_pair;
    tmp_pair.first=0; tmp_pair.second=0;
    std_map_indicies[0] = tmp_pair;

    tmp_pair.first=0; tmp_pair.second=1;
    std_map_indicies[1] = tmp_pair;

    tmp_pair.first=1; tmp_pair.second=1;
    std_map_indicies[2] = tmp_pair;        
}
else
{
    throw std::runtime_error("only dim==2 or dim==3 allowed");
}

Instead of calling the *.diff(*) on the components one-by-one we could also use the following for-loop, so we also use the map to set the dofs (as we will do in the Wrapper later).

for ( unsigned int x=0; x<((dim==2)?3:6); ++x )
{
    unsigned int i=std_map_indicies[x].first;
    unsigned int j=std_map_indicies[x].second;
    eps[i][j].diff(x,((dim==2)?3:6));
}

For our slightly more complicated stress equation we need the unit and deviatoric tensors. We can simply define them by writing the values of the already existing deal.ii functions into newly defined SymmetricTensors build from fad_doubles.

SymmetricTensor<2,dim, fad_double> stdTensor_I (( unit_symmetric_tensor<dim,fad_double>()) );
SymmetricTensor<4,dim, fad_double> stdTensor_Idev ( (deviator_tensor<dim,fad_double>()) );

With everything set and defined, we can compute our stress sigma according to:

\[ \sigma = \kappa \cdot trace(\varepsilon) \cdot \boldsymbol{I} + 2 \cdot \mu \cdot \varepsilon^{dev} \]

Here you can see that we can directly multiply the constant and the tensors when kappa is also declared as fad_double

sigma = kappa * (trace(eps) *  stdTensor_I);

We didn't do the same for mu to once again emphasize the difference between constants as double and as fad_double.
The remaining code uses a normal double constant.

SymmetricTensor<2,dim,fad_double> tmp = deviator<dim,fad_double>(symmetrize<dim,fad_double>(eps)); tmp*=(mu*2);
sigma +=  tmp;

The fairly cumbersome computation is caused by the way the operators are set up for tensors out of fad_doubles.

std::cout << "sigma=" << sigma << std::endl;

Now we want to actually build our tangent modulus called C_Sacado that contains all the derivatives and relates the stress tensor with the strain tensor.
The fourth-order tensor C_Sacado is our final goal, we don't have to compute anything that is related to Sacado with this tensor, so we can finally return to our standard SymmetricTensor out of doubles. The latter is necessary to use the tangent in the actual FE code.

SymmetricTensor<4,dim> C_Sacado;

As in example 2 we access the components of the stress tensor one by one. In order to capture all of them we loop over the components i and j of the stress tensor.

for ( unsigned int i=0; i<dim; ++i)
    for ( unsigned int j=0; j<dim; ++j )
    {
        double *derivs = &sigma[i][j].fastAccessDx(0); // Access the derivatives of the (i,j)-th component of \a sigma

To visually ensure that every stress component has in fact all 6 derivatives for 3D or 3 for 2D, we output the size:

std::cout<<"size: "<<sigma[i][j].size()<<std::endl;

We loop over all the dofs. To be able to use this independent of the chosen dimension dim, we use a ternary operator to decide whether we have to loop over 6 derivatives or just 3.

    for(unsigned int x=0;x<((dim==2)?3:6);++x)
    {
        unsigned int k=std_map_indicies[x].first;
        unsigned int l=std_map_indicies[x].second;

        if(k!=l)/*Compare to Voigt notation since only SymmetricTensor instead of Tensor*/
        {
            C_Sacado[i][j][k][l] = 0.5*derivs[x];
            C_Sacado[i][j][l][k] = 0.5*derivs[x];
        }
        else
            C_Sacado[i][j][k][l] = derivs[x];
    }            

}

After resembling the fourth-order tensor, we now have got our tangent saved in C_Sacado ready to be used

To ensure that Sacado works properly, we can compute the analytical tangent for comparison

double kappa_d = 5;
double mu_d = 2;

Our stress equation in this example is still simple enough to derive the tangent analytically by hand:

\[ \overset{4}{C_{analy}} = \kappa \cdot \boldsymbol{I} \otimes \boldsymbol{I} + 2 \cdot \mu \cdot \overset{4}{I^{dev}} \]

SymmetricTensor<4,dim> C_analy = kappa_d * outer_product(unit_symmetric_tensor<dim>(), unit_symmetric_tensor<dim>()) + 2* mu_d * deviator_tensor<dim>();

We again define our strain tensor eps_d (*_d for standard double in contrast to fad_double)

SymmetricTensor<2,dim> eps_d;

if(dim==3)
{
    eps_d[0][0] = 1;
    eps_d[1][1] = 2;
    eps_d[2][2] = 3;

    eps_d[0][1] = 4;
    eps_d[0][2] = 5;
    eps_d[2][1] = 6;

}
else if(dim==2)
{
    eps_d[0][0] = 1;
    eps_d[1][1] = 2;

    eps_d[1][0] = 4;

}
else
{
    throw std::runtime_error("only dim==2 or dim==3 allowed");
}

Todo:

use boldsymbol for tensors

To output the stress tensor we first have to compute it. We do this here via

\[ \sigma = \overset{4}{C_{analy}} : \varepsilon \]

The output exactly matched the result obtained with Sacado.

Note

Checking the Sacado stress tensor against an analytically computed or otherwise determined stress tensor is absolutely no way to check whether the tangent computed via Sacado is correct. When we compute the stress tensor with Sacado and for example mix up a + and - sign, this might not matter at all if the number that is added or subtracted is small. However, for the tangent this nasty sign can be very critical. Just keep in mind: the tangent has 81 components and the stress tensor just 9, so how does one want to verify 81 variables by comparing 9?

std::cout << "sigma_analy: " << (C_analy*eps_d) << std::endl;

That's the reason we compare all the entries in the Sacado and the analytical tensor one by one

for (unsigned int i=0; i<dim; ++i)
    for ( unsigned int j=0; j<dim; ++j)
        for ( unsigned int k=0; k<dim; ++k)
            for ( unsigned int l=0; l<dim; ++l)
                std::cout << "C_analy["<<i<<"]["<<j<<"]["<<k<<"]["<<l<<"] = " << C_analy[i][j][k][l] << " vs C_Sacado: " << C_Sacado[i][j][k][l] << std::endl;

To simplify the comparison we compute a scalar error as the sum of the absolute differences of each component

double error_Sacado_vs_analy=0;
for (unsigned int i=0; i<dim; ++i)
    for ( unsigned int j=0; j<dim; ++j)
        for ( unsigned int k=0; k<dim; ++k)
            for ( unsigned int l=0; l<dim; ++l)
                error_Sacado_vs_analy += std::fabs(C_Sacado[i][j][k][l] - C_analy[i][j][k][l]);

As desired: The numerical error is zero (0 in double precision) and the tensor components are equal

    std::cout << "numerical error: " << error_Sacado_vs_analy << std::endl;
}

3B. Example: Using the wrapper for Ex3

void sacado_test_3B ()
{
    std::cout << "Test 3B:" << std::endl;
    const unsigned int dim=3;

The following declarations are usually input arguments. So you receive the strain tensor and the constants out of doubles.

SymmetricTensor<2,dim> eps_d;
eps_d[0][0] = 1;
eps_d[1][1] = 2;
eps_d[2][2] = 3;

eps_d[0][1] = 4;
eps_d[0][2] = 5;
eps_d[1][2] = 6;

double kappa = 5;
double mu = 2;

Now we start working with Sacado:
When we use the index notation to compute e.g. our stress we do not need to declare our constants (here kappa, mu) as fad_double.

We declare our strain tensor as the special data type Sacado_Wrapper::SymTensor from the file "Sacado_Wrapper.h" where this data type was derived from the SymmetricTensor<2,dim,fad_double>.

Sacado_Wrapper::SymTensor<dim> eps;

Next we initialize our Sacado strain tensor with the values of the inputed double strain tensor:

eps.init(eps_d);

We define all the entries in the symmetric tensor eps as the dofs. So we can later derive any variable with respect to the strain tensor eps.

Note

Keep the order first declare eps, then initialise it and afterwards set it as dofs

eps.set_dofs();

Now we declare our output and auxiliary variables as Sacado-Tensors.

SymmetricTensor<2,dim,fad_double> sigma;

SymmetricTensor<2,dim, fad_double> stdTensor_I (( unit_symmetric_tensor<dim,fad_double>()) );

Our stress equation is now computed in index notation to simplify the use of the constants and especially the use of the deviator.

for ( unsigned int i=0; i<dim; ++i)
  for ( unsigned int j=0; j<dim; ++j )
      sigma[i][j] = kappa * trace(eps) *  stdTensor_I[i][j] + 2. * mu * deviator(eps)[i][j];

Finally we declare our desired tangent as the fourth order tensor C_Sacado and compute the tangent via the command get_tangent.

SymmetricTensor<4,dim> C_Sacado;
eps.get_tangent(C_Sacado, sigma);

We could again compare the herein computed tangent with the analytical tangent from Ex2, but as before the results are fairly boring, because Sacado hits the analytical tangent exactly — no surprise for such simple equations.

And that's it. By using the Sacado_wrapper we can achieve everything from Ex2 (besides the equations) with just four lines of code namely:

• eps.init(eps_d); // To initialize the Sacado strain tensor
• eps.set_dofs(); // To declare the components of eps as the dofs
• eps.get_tangent(*); // To get the tangent

  }

4. Example: Computing derivatives with respect to a tensor and a scalar

void sacado_test_4 ()
{
    std::cout << "Test 4:" << std::endl;
    const unsigned int dim=3;

The following declarations are usually input arguments. So you receive the strain tensor eps_d, the damage variable phi and the constants kappa and mu out of doubles.

SymmetricTensor<2,dim> eps_d;
eps_d[0][0] = 1;
eps_d[1][1] = 2;
eps_d[2][2] = 3;

eps_d[0][1] = 4;
eps_d[0][2] = 5;
eps_d[1][2] = 6;

double phi_d = 0.3;

We don't need these constants in the current example. double kappa = 5; double mu = 2;

We set up our strain tensor as in Ex3B.

Sacado_Wrapper::SymTensor<dim> eps;
Sacado_Wrapper::SW_double<dim> phi;

Initialize the strain tensor and the damage variable

eps.init(eps_d);
phi.init(phi_d);

Set the dofs, where the argument sets the total nbr of dofs (3 or 6 for the sym. tensor and 1 for the double)

//    eps.set_dofs(eps.n_independent_components+1/*an additional dof for phi*/);
//

In order to also compute derivatives with respect to the scalar phi, we add this scalar to our list of derivatives. Because we have already defined 3 or 6 dofs our additional dof will be placed at the end of this list. We set this up with the member variable start_index ...

//    phi.start_index=eps.n_independent_components;

and again using the input argument representing the total number of dofs

//    phi.set_dofs(eps.n_independent_components+1);

All of the above 3 lines of code are automatically done by the DoFs_summary class. So, to set our dofs we just create an instance and call set_dofs with our variables containing the desired dofs.

Sacado_Wrapper::DoFs_summary<dim> DoFs_summary;
DoFs_summary.set_dofs(eps, phi);

Compute the stress tensor and damage variable d (here we just use some arbitrary equations for testing):
Let us first declare our output (and auxiliary) variables as Sacado data types.

SymmetricTensor<2,dim,fad_double> sigma;
fad_double d;

Todo:

It would be nice to use the data types from the Sacado_Wrapper for all the Sacado variables. But somehow the operators (multiply*, ...) seem to cause conflicts again.

The actual computation in the following scope uses the exact same equation as your normal computation e. g. via the data type double. Hence, you could either directly compute your stress, etc. via the Sacado variables or you define template functions that contain your equations and are either called templated with double or fad_double. When using the first option, please consider the computation time that is generally higher for a computation with fad_double than with normal doubles (own experience in a special case: slower by factor 30). The second option with templates does not suffer these issues.

{
d = phi*phi + 25 + trace(eps) + eps.norm();
std::cout << "d=" << d << std::endl;

for ( unsigned int i=0; i<dim; ++i)
  for ( unsigned int j=0; j<dim; ++j )
      sigma[i][j] = phi * d * eps[i][j];

ToDo: strangely when phi is a fad_double then the multiplication phi * eps works directly without having to use the index notation

std::cout << "sigma=" << sigma << std::endl << std::endl;
}

Get the tangents d_sigma / d_eps: SymmetricTensor with respect to SymmetricTensor

SymmetricTensor<4,dim> C_Sacado;
eps.get_tangent(C_Sacado, sigma);
std::cout << "C_Sacado=" << C_Sacado << std::endl;

Compute the analytical tangent:

SymmetricTensor<4,dim> C_analy;
C_analy = ( std::pow(phi_d, 3) + 25*phi_d + phi_d*trace(eps_d) + phi_d*eps_d.norm() ) * identity_tensor<dim>()
          + phi_d * outer_product( eps_d, unit_symmetric_tensor<dim>())
          + phi_d * outer_product( eps_d, eps_d ) * 1./eps_d.norm();

Note

Be aware of the difference between

\[ eps_d \otimes \boldsymbol{1} \text{ and } \boldsymbol{1} \otimes eps_d \]

std::cout << "C_analy =" << C_analy << std::endl;

To simplify the comparison we compute a scalar error as the sum of the absolute differences of each component

double error_Sacado_vs_analy=0;
for (unsigned int i=0; i<dim; ++i)
     for ( unsigned int j=0; j<dim; ++j)
         for ( unsigned int k=0; k<dim; ++k)
             for ( unsigned int l=0; l<dim; ++l)
                 error_Sacado_vs_analy += std::fabs(C_Sacado[i][j][k][l] - C_analy[i][j][k][l]);
std::cout << "numerical error: " << error_Sacado_vs_analy << std::endl << std::endl;

d_d / d_eps: double with respect to SymmetricTensor

SymmetricTensor<2,dim> d_d_d_eps;
eps.get_tangent(d_d_d_eps, d);
std::cout << "d_d_d_eps      =" << d_d_d_eps << std::endl;
SymmetricTensor<2,dim> d_d_d_eps_analy;
d_d_d_eps_analy = unit_symmetric_tensor<dim>() + eps_d / eps_d.norm();
std::cout << "d_d_d_eps_analy=" << d_d_d_eps_analy << std::endl << std::endl;

d_sigma / d_phi: SymmetricTensor with respect to double

SymmetricTensor<2,dim> d_sigma_d_phi;
phi.get_tangent(d_sigma_d_phi, sigma);
std::cout << "d_sigma_d_phi      =" << d_sigma_d_phi << std::endl;
SymmetricTensor<2,dim> d_sigma_d_phi_analy;
d_sigma_d_phi_analy = ( phi_d*phi_d + 25 + trace(eps_d) + eps_d.norm() + 2 * phi_d*phi_d ) * eps_d;
std::cout << "d_sigma_d_phi_analy=" << d_sigma_d_phi_analy << std::endl << std::endl;

Retrieve the values stored in sigma:

SymmetricTensor<2,dim> sigma_d;
for ( unsigned int i=0; i<dim; ++i)
      for ( unsigned int j=0; j<dim; ++j )
          sigma_d[i][j] = sigma[i][j].val();
std::cout << "sigma_d = " << sigma_d << std::endl;

d_d / d_phi: double with respect to double

double d_d_d_phi;
phi.get_tangent(d_d_d_phi, d);
std::cout << "d_d_d_phi=" << d_d_d_phi << std::endl;

Retrieve the value stored in d

double d_double = d.val();

Taylor-series for point x

Todo:

Maybe add some more text on the linearization

double x = phi_d + 0.05;
std::cout << "d_lin = d_d_d_phi * (phi_d - x) + d@(phi_d) = " << d_d_d_phi * (x-phi_d) + d_double << std::endl;
std::cout << "d@x = " << x*x + 25 + trace(eps_d) + eps_d.norm() << std::endl;

And that's it. By using the Sacado_wrapper we can compute derivatives with respect to a tensor and a scalar at the same time (besides the equations) in essence with just the following lines of code namely:

• eps.init(eps_d); phi.init(phi_d); // To initialize the Sacado strain tensor and scalar damage variable
• DoFs_summary.set_dofs(eps, phi); // To declare the components of eps and phi as the dofs
• eps.get_tangent(*); // To get tangents with respect to eps
• phi.get_tangent(*); // To get tangents with respect to phi

  }

5. Example: Using a vector-valued equation

void sacado_test_5 ()
{
    const unsigned int dim=3;
    std::cout << "Test 5:" << std::endl;
    Tensor<1,dim,fad_double> c;
    fad_double a,b;
    unsigned int n_dofs=2;
    a = 1; b = 2;   // at the point (a,b) = (1,2)
    a.diff(0,2);  // Set a to be dof 0, in a 2-dof system.
    b.diff(1,2);  // Set b to be dof 1, in a 2-dof system.

c is now a vector with three components

c[0] = 2*a+3*b;
c[1] = 4*a+5*b;
c[2] = 6*a+7*b;

Access to the derivatives works as before.

    for(unsigned int i=0;i<dim;++i)
    {
        const fad_double &derivs = c[i]; // Access derivatives
        for(unsigned int j=0;j<n_dofs;++j)
        {
            std::cout << "Derivatives at the point (" << a << "," << b << ") for "
            <<i<<"th component wrt "<<j<<"th direction "<< std::endl;
            std::cout << "dc_i/dxj = " << derivs.fastAccessDx(j) << std::endl;            
        }
    }
}

6. Example: First and second derivatives - Scalar equation

The here shown example was copied from https://github.com/trilinos/Trilinos/blob/master/packages/sacado/example/dfad_dfad_example.cpp and modified to get a first impression on how we can work with first and second derivatives

void sacado_test_6 ()
{
    std::cout << "Test 6:" << std::endl;

Define the variables used in the computation (inputs: a, b; output: c; auxiliaries: *) as doubles

double a=1;
double b=2;

Number of independent variables (scalar a and b)

int num_dofs = 2;

Define another data type containing even more Sacado data types

Todo:

try to merge the fad_double data type with this templated data type

typedef Sacado::Fad::DFad<double> DFadType;
Sacado::Fad::DFad<DFadType> afad(num_dofs, 0, a);
Sacado::Fad::DFad<DFadType> bfad(num_dofs, 1, b);
Sacado::Fad::DFad<DFadType> cfad;

Output the variables: We se that the values of a and b are set but the derivatives have not yet been fully declared

std::cout << "afad=" << afad << std::endl;
std::cout << "bfad=" << bfad << std::endl;
std::cout << "cfad=" << cfad << std::endl;

Now we set the "inner" derivatives.

afad.val() = fad_double(num_dofs, 0, a); // set afad.val() as the first dof and init it with the double a
bfad.val() = fad_double(num_dofs, 1, b);

Compute function and derivative with AD

cfad = 2*afad + std::cos(afad*bfad);

After this, we output the variables again and see that some additional derivatives have been declared. Furthermore, cfad is filled with the values and derivatives

std::cout << "afad=" << afad << std::endl;
std::cout << "bfad=" << bfad << std::endl;
std::cout << "cfad=" << cfad << std::endl;

Extract value and derivatives

double c_ad = cfad.val().val();       // r
double dcda_ad = cfad.dx(0).val();    // dr/da
double dcdb_ad = cfad.dx(1).val();    // dr/db
double d2cda2_ad = cfad.dx(0).dx(0);  // d^2r/da^2
double d2cdadb_ad = cfad.dx(0).dx(1); // d^2r/dadb
double d2cdbda_ad = cfad.dx(1).dx(0); // d^2r/dbda
double d2cdb2_ad = cfad.dx(1).dx(1);  // d^2/db^2

Now we can print the actual double value of c and some of the derivatives:

     std::cout << "c_ad=" << c_ad << std::endl;
     std::cout << "Derivatives at the point (" << a << "," << b << ")" << std::endl;
     std::cout << "dc/da = " << dcda_ad << ", dc/db=" << dcdb_ad << std::endl;
     std::cout << "d²c/da² = " << d2cda2_ad << ", d²c/db²=" << d2cdb2_ad << std::endl;
     std::cout << "d²c/dadb = " << d2cdadb_ad << ", d²c/dbda=" << d2cdbda_ad << std::endl;
}

7. Example: First and second derivatives - Using tensors (The full story)

void sacado_test_7 ()
{
    const unsigned int dim=3;
 
    std::cout << "Test 7:" << std::endl;

Defining the inputs (material parameters, strain tensor)

double lambda=1;
double mu=2;
SymmetricTensor<2,dim, double> eps;

eps[0][0] = 1.;
eps[1][1] = 2.;
eps[2][2] = 3.;

eps[0][1] = 4.;
eps[0][2] = 5.;
eps[1][2] = 6.;

Here we skip the one-field example and right away show the equations for a two-field problem with eps and phi.

double phi=0.3;

Setup of the map relating the indices (as before)

std::map<unsigned int,std::pair<unsigned int,unsigned int>> std_map_indicies;

std::pair<unsigned int, unsigned int> tmp_pair;
tmp_pair.first=0; tmp_pair.second=0;
std_map_indicies[0] = tmp_pair;

tmp_pair.first=0; tmp_pair.second=1;
std_map_indicies[1] = tmp_pair;

tmp_pair.first=0; tmp_pair.second=2;
std_map_indicies[2] = tmp_pair;

tmp_pair.first=1; tmp_pair.second=1;
std_map_indicies[3] = tmp_pair;

tmp_pair.first=1; tmp_pair.second=2;
std_map_indicies[4] = tmp_pair;

tmp_pair.first=2; tmp_pair.second=2;
std_map_indicies[5] = tmp_pair;

Number of independent variables (6 for the tensor and 1 for the scalar phi)

const unsigned int nbr_dofs = 6+1;

Declaring the special data types containing all derivatives

typedef Sacado::Fad::DFad<double> DFadType;
SymmetricTensor<2,dim, Sacado::Fad::DFad<DFadType> > eps_fad, eps_fad_squared;
Sacado::Fad::DFad<DFadType> phi_fad;

Setting the dofs

for ( unsigned int x=0; x<6; ++x )
{
   unsigned int i=std_map_indicies[x].first;
   unsigned int j=std_map_indicies[x].second;
   (eps_fad[i][j]).diff( x, nbr_dofs); // set up the "inner" derivatives
   (eps_fad[i][j]).val() = fad_double(nbr_dofs, x, eps[i][j]); // set up the "outer" derivatives
}

phi_fad.diff( 6, nbr_dofs );
phi_fad.val() = fad_double(nbr_dofs, 6, phi); // set up the "outer" derivatives

std::cout << "eps_fad=" << eps_fad << std::endl;
std::cout << "phi_fad=" << phi_fad << std::endl;

Compute eps² = eps_ij * eps_jk in index notation

for ( unsigned int i=0; i<dim; ++i)
   for ( unsigned int k=0; k<dim; ++k )
       for ( unsigned int j=0; j<dim; ++j )
           if ( i>=k )
               eps_fad_squared[i][k] += eps_fad[i][j] * eps_fad[j][k];

Compute the strain energy density

Sacado::Fad::DFad<DFadType> energy;
energy = lambda/2. * trace(eps_fad)*trace(eps_fad) + mu * trace(eps_fad_squared) + 25 * phi_fad * trace(eps_fad);

Give some insight into the storage of the values and derivatives

std::cout << "energy=" << energy << std::endl;

Compute sigma as

\[ \frac{\partial \Psi}{\partial \boldsymbol{\varepsilon}} \]

SymmetricTensor<2,dim> sigma_Sac;
for ( unsigned int x=0; x<6; ++x )
{
   unsigned int i=std_map_indicies[x].first;
   unsigned int j=std_map_indicies[x].second;
   if ( i!=j )
       sigma_Sac[i][j] = 0.5 * energy.dx(x).val();
   else
       sigma_Sac[i][j] = energy.dx(x).val();
}
std::cout << "sigma_Sacado=" << sigma_Sac << std::endl;

double d_energy_d_phi = energy.dx(6).val();
std::cout << "d_energy_d_phi=" << d_energy_d_phi << std::endl;

double d2_energy_d_phi_2 = energy.dx(6).dx(6);
std::cout << "d2_energy_d_phi_2=" << d2_energy_d_phi_2 << std::endl;

Analytical stress tensor:

SymmetricTensor<2,dim> sigma;
sigma = lambda*trace(eps)*unit_symmetric_tensor<dim>() + 2. * mu * eps + 25 * phi * unit_symmetric_tensor<dim>();
std::cout << "analy. sigma=" << sigma << std::endl;

Sacado-Tangent

SymmetricTensor<4,dim> C_Sac;
for(unsigned int x=0;x<6;++x)
   for(unsigned int y=0;y<6;++y)
   {
       const unsigned int i=std_map_indicies[y].first;
       const unsigned int j=std_map_indicies[y].second;
       const unsigned int k=std_map_indicies[x].first;
       const unsigned int l=std_map_indicies[x].second;

       double deriv = energy.dx(x).dx(y); // Access the derivatives of the (i,j)-th component of \a sigma

       if ( k!=l && i!=j )
           C_Sac[i][j][k][l] = 0.25* deriv;
       else if(k!=l)/*Compare to Voigt notation since only SymmetricTensor instead of Tensor*/
       {
           C_Sac[i][j][k][l] = 0.5*deriv;
           C_Sac[i][j][l][k] = 0.5*deriv;
       }
       else
           C_Sac[i][j][k][l] = deriv;
   }

Analytical tangent

     SymmetricTensor<4,dim> C_analy;
     C_analy = lambda * outer_product(unit_symmetric_tensor<dim>(), unit_symmetric_tensor<dim>()) + 2. * mu * identity_tensor<dim>();
 
    double error_Sacado_vs_analy=0;
    for (unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j)
            for ( unsigned int k=0; k<dim; ++k)
                for ( unsigned int l=0; l<dim; ++l)
                    error_Sacado_vs_analy += std::fabs(C_Sac[i][j][k][l] - C_analy[i][j][k][l]);
 
    std::cout << "Numerical error=" << error_Sacado_vs_analy << std::endl;
}

8. Example: First and second derivatives - Using the Wrapper

void sacado_test_8 ()
 
{
    const unsigned int dim=3;
 
    std::cout << "Test 8:" << std::endl;

Defining the inputs (material parameters, strain tensor)

double lambda=1;
double mu=2;
SymmetricTensor<2,dim, double> eps;
double phi = 0.3;

eps[0][0] = 1.;
eps[1][1] = 2.;
eps[2][2] = 3.;

eps[0][1] = 4.;
eps[0][2] = 5.;
eps[1][2] = 6.;

Declaring the special data types containing all derivatives

typedef Sacado::Fad::DFad<double> DFadType;

Declare the variables eps_fad and phi_fad as the special Wrapper data types

Sacado_Wrapper::SymTensor2<dim> eps_fad;
Sacado_Wrapper::SW_double2<dim> phi_fad;

Declare the summary data type relating all the dofs and initialising them too

Sacado_Wrapper::DoFs_summary<dim> DoFs_summary;
DoFs_summary.init_set_dofs(eps_fad, eps, phi_fad, phi);

The variables are outputted to give some insight into the storage of the values (derivatives still trivial).

std::cout << "eps_fad=" << eps_fad << std::endl;
std::cout << "phi_fad=" << phi_fad << std::endl;

Compute eps² = eps_ij * eps_jk in index notation

SymmetricTensor<2,dim, Sacado::Fad::DFad<DFadType> > eps_fad_squared;
for ( unsigned int i=0; i<dim; ++i)
   for ( unsigned int k=0; k<dim; ++k )
       for ( unsigned int j=0; j<dim; ++j )
           if ( i>=k )
               eps_fad_squared[i][k] += eps_fad[i][j] * eps_fad[j][k];

Compute the strain energy density

Sacado::Fad::DFad<DFadType> energy;
energy = lambda/2. * trace(eps_fad)*trace(eps_fad) + mu * trace(eps_fad_squared) + 25 * phi_fad * trace(eps_fad);

The energy is outputted (formatted by hand) to give some insight into the storage of the values and derivatives.
energy=399 [ 17.5 32 40 21.5 48 25.5 150 ]
[ 17.5 [ 5 0 0 1 0 1 25 ] 32 [ 0 8 0 0 0 0 0 ] 40 [ 0 0 8 0 0 0 0 ]
21.5 [ 1 0 0 5 0 1 25 ] 48 [ 0 0 0 0 8 0 0 ] 25.5 [ 1 0 0 1 0 5 25 ]
150 [ 25 0 0 25 0 25 0 ] ]

std::cout << "energy=" << energy << std::endl;

Compute sigma as

\[ \boldsymbol{\sigma} = \frac{\partial \Psi}{\partial \boldsymbol{\varepsilon}} \]

SymmetricTensor<2,dim> sigma_Sac;
eps_fad.get_tangent(sigma_Sac, energy);
std::cout << "sigma_Sacado=" << sigma_Sac << std::endl;

double d_energy_d_phi;
phi_fad.get_tangent(d_energy_d_phi, energy);
std::cout << "d_energy_d_phi=" << d_energy_d_phi << std::endl;

Analytical stress tensor:

SymmetricTensor<2,dim> sigma;
sigma = lambda*trace(eps)*unit_symmetric_tensor<dim>() + 2. * mu * eps + 25 * phi * unit_symmetric_tensor<dim>();
std::cout << "analy. sigma=" << sigma << std::endl;

Sacado stress tangent (or eps curvature) as

\[ \frac{\partial^2 \Psi}{\partial \boldsymbol{\varepsilon}^2} \]

SymmetricTensor<4,dim> C_Sac;
eps_fad.get_curvature(C_Sac, energy);

Sacado phi curvature as

\[ \frac{\partial^2 \Psi}{\partial \varphi^2} \]

double d2_energy_d_phi_2;
phi_fad.get_curvature(d2_energy_d_phi_2, energy);
std::cout << "d2_energy_d_phi_2=" << d2_energy_d_phi_2 << std::endl;

Sacado derivatives

\[ \frac{\partial^2 \Psi}{\partial \boldsymbol{\varepsilon} \partial \varphi} \]

SymmetricTensor<2,dim> d2_energy_d_eps_d_phi;
DoFs_summary.get_curvature(d2_energy_d_eps_d_phi, energy, eps_fad, phi_fad);
std::cout << "d2_energy_d_eps_d_phi=" << d2_energy_d_eps_d_phi << std::endl;

Sacado derivatives

\[ \frac{\partial^2 \Psi}{\partial \varphi \partial \boldsymbol{\varepsilon}} \]

SymmetricTensor<2,dim> d2_energy_d_phi_d_eps;
DoFs_summary.get_curvature(d2_energy_d_phi_d_eps, energy, phi_fad, eps_fad);
std::cout << "d2_energy_d_phi_d_eps=" << d2_energy_d_phi_d_eps << std::endl;

When you consider the output:
d2_energy_d_eps_d_phi=25 0 0 0 25 0 0 0 25
d2_energy_d_phi_d_eps=25 0 0 0 25 0 0 0 25
in detail you will notice that both second derivatives are identical. This compplies with the Schwarz integrability condition (Symmetry of second derivatives) (ignoring all limitation and requirements), it holds

\[ \frac{\partial^2 \Psi}{\partial \boldsymbol{\varepsilon} \partial \varphi} = \frac{\partial^2 \Psi}{\partial \varphi \partial \boldsymbol{\varepsilon}} \]

Analytical stress tangent

SymmetricTensor<4,dim> C_analy;
C_analy = lambda * outer_product(unit_symmetric_tensor<dim>(), unit_symmetric_tensor<dim>()) + 2. * mu * identity_tensor<dim>();

Compute the error for the stress tangent

     double error_Sacado_vs_analy=0;
     for (unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j)
            for ( unsigned int k=0; k<dim; ++k)
                for ( unsigned int l=0; l<dim; ++l)
                    error_Sacado_vs_analy += std::fabs(C_Sac[i][j][k][l] - C_analy[i][j][k][l]);
     std::cout << "Numerical error=" << error_Sacado_vs_analy << std::endl;
}

9. Example: Why we sometimes need the factor of 0.5 in the derivatives and sometimes we don't

void sacado_test_9 ()
 
{
    const unsigned int dim=3;
 
    std::cout << "Test 9:" << std::endl;
 
    double kappa_param = 5;
    fad_double kappa (kappa_param);
    double mu = 2;
 
    SymmetricTensor<2,dim, fad_double> sigma, eps;
 
    std::map<unsigned int,std::pair<unsigned int,unsigned int>> std_map_indicies;
 
        eps[0][0] = 1;
        eps[1][1] = 2;
        eps[2][2] = 3;
 
        eps[0][1] = 4;
        eps[0][2] = 5;
        eps[1][2] = 6;
 
 
        eps[0][0].diff(0,6);
        eps[0][1].diff(1,6);
        eps[0][2].diff(2,6);
        eps[1][1].diff(3,6);
        eps[1][2].diff(4,6);
        eps[2][2].diff(5,6);
 
        std::pair<unsigned int, unsigned int> tmp_pair;
        tmp_pair.first=0; tmp_pair.second=0;
        std_map_indicies[0] = tmp_pair;
 
        tmp_pair.first=0; tmp_pair.second=1;
        std_map_indicies[1] = tmp_pair;
 
        tmp_pair.first=0; tmp_pair.second=2;
        std_map_indicies[2] = tmp_pair;
 
        tmp_pair.first=1; tmp_pair.second=1;
        std_map_indicies[3] = tmp_pair;
 
        tmp_pair.first=1; tmp_pair.second=2;
        std_map_indicies[4] = tmp_pair;
 
        tmp_pair.first=2; tmp_pair.second=2;
        std_map_indicies[5] = tmp_pair;
 
    SymmetricTensor<2,dim, fad_double> stdTensor_I (( unit_symmetric_tensor<dim,fad_double>()) );
 
    sigma = kappa * (trace(eps) *  stdTensor_I);
    SymmetricTensor<2,dim,fad_double> tmp = deviator<dim,fad_double>(symmetrize<dim,fad_double>(eps)); tmp*=(mu*2);
    sigma +=  tmp;
 
    std::cout << "sigma=" << sigma << std::endl;

Retrieve the values stored in sigma:

  SymmetricTensor<2,dim> sigma_d;
  for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
            sigma_d[i][j] = sigma[i][j].val();

SymmetricTensor<4,dim> C_Sacado;

for ( unsigned int i=0; i<dim; ++i)
    for ( unsigned int j=0; j<dim; ++j )
    {
        double *derivs = &sigma[i][j].fastAccessDx(0); // Access the derivatives of the (i,j)-th component of \a sigma

        for(unsigned int x=0;x<((dim==2)?3:6);++x)
        {
            unsigned int k=std_map_indicies[x].first;
            unsigned int l=std_map_indicies[x].second;

            if(k!=l)/*Compare to Voigt notation since only SymmetricTensor instead of Tensor*/
            {
                C_Sacado[i][j][k][l] = 0.5*derivs[x];
                C_Sacado[i][j][l][k] = 0.5*derivs[x];
            }
            else
                C_Sacado[i][j][k][l] = derivs[x];
        }
    }

SymmetricTensor<2,dim> eps_d;
eps_d[0][0] = 1;
eps_d[1][1] = 2;
eps_d[2][2] = 3;

eps_d[0][1] = 4;
eps_d[0][2] = 5;
eps_d[1][2] = 6;

SymmetricTensor<2,dim> stress_from_tangent = C_Sacado*eps_d;

std::cout << "C_Sacado*eps_d=" << stress_from_tangent << std::endl;
std::cout << "sigma=         " << sigma_d << std::endl;

Todo:

Add the link to the ac.nz site

As you can see we obtain the correct stress tensor only by using the factor 0.5 onto the off-diagonal elements of the symmetric tensor.

Note

So, why do we need the factor 0.5 then? (based on [homepages.engineering.auckland.ac.nz ...])
When using symmetric tensor one has to be aware of the definition of the independent variables. In 3d those are the following 6 components:

• \( A_{11} \)
• \( A_{22} \)
• \( A_{33} \)
• \( \overline{A_{12}} \)
• \( \overline{A_{13}} \)
• \( \overline{A_{23}} \)
  Here the overlined components denote the averaged values, such that
• \( \overline{A_{12}} = 0.5 \cdot [ A_{12} + A_{21} ] = A_{12} = A_{21} \)
• ...
  This looks rather boring, because the averaged value of the two identical components (symmetry) is identical to the components. But (and that is a crucial BUT), this only holds for the values NOT the derivatives. The derivative of a function \( \Phi \) with respect to a symmetric tensor A is

  \[ \frac{\partial \Phi}{\partial \overline{A_{12}}} = \frac{\partial \Phi}{\partial A_{12}} \cdot \frac{\partial A_{12}}{\partial \overline{A_{12}}} + \frac{\partial \Phi}{\partial A_{21}} \cdot \frac{\partial A_{21}}{\partial \overline{A_{21}}} = \frac{\partial \Phi}{\partial A_{12}} + \frac{\partial \Phi}{\partial A_{21}} = 2 \cdot \frac{\partial \Phi}{\partial A_{12}} \]

  Note how the derivatives with respect to the actual tensor components (here 12 and 21) are identical.
  However, our derivatives (computed via Sacado) were calculated with respect to the actually independent variables (overlined). Still, in the tensor with the derivatives we want the derivatives with respect to the normal components (not overlined).
  Summary:
  When you compute derivatives with respect to a symmetric tensor, you have to scale the off-diagonal elements by 0.5 to account for the fact that you actually work with the averaged values.
  As a consequence, we use the factor 0.5 for all off-diagonal components of derivatives with respect to symmetric tensors. For second derivatives with respect to symmetric tensors the factors 0.5 and 0.25 come into play.

}

Note

Here we template <dim,Number> for a function "on the same level". If you template a member function with <Number> inside a class template <dim>, use

template<int dim>
template<typename Number>
SymmetricTensor<2,dim,Number> ...

For the latter the declaration of the member function in the class body looks like this:

 template<typename Number>
SymmetricTensor<2,dim,Number> ...

template<int dim, typename Number>
SymmetricTensor<2,dim,Number> stress_strain_relation ( const SymmetricTensor<2,dim,Number> &eps, const double &kappa, const double &mu )
{
    SymmetricTensor<2,dim,Number> sigma;
 
    SymmetricTensor<2,dim,Number> stdTensor_I (( unit_symmetric_tensor<dim,Number>()) );

Our stress equation is now computed in index notation to simplify the use of the constants and especially the use of the deviator.

     for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
            sigma[i][j] = kappa * trace(eps) *  stdTensor_I[i][j] + 2. * mu * deviator(eps)[i][j];
 
    return sigma;
}

10. Example: Using the wrapper with templated functions

void sacado_test_10 ()
{
    std::cout << "Test 10:" << std::endl;
    const unsigned int dim=3;

To measure the computation time of certain sections (see below)

TimerOutput timer (std::cout, TimerOutput::summary, TimerOutput::cpu_times);

The following declarations are usually input arguments. So you receive the strain tensor and the constants out of doubles.

SymmetricTensor<2,dim> eps_d;
eps_d[0][0] = 1;
eps_d[1][1] = 2;
eps_d[2][2] = 3;

eps_d[0][1] = 4;
eps_d[0][2] = 5;
eps_d[1][2] = 6;

double kappa = 5;
double mu = 2;

Now we start working with Sacado:
When we use the index notation to compute e.g. our stress we do not need to declare our constants (here kappa, mu) as fad_double.

We declare our strain tensor as the special data type Sacado_Wrapper::SymTensor from the file "Sacado_Wrapper.h" where this data type was derived from the SymmetricTensor<2,dim,fad_double>.

Sacado_Wrapper::SymTensor<dim> eps;

Next we initialize our Sacado strain tensor with the values of the inputed double strain tensor:

eps.init(eps_d);

We define all the entries in the symmetric tensor eps as the dofs. So we can later derive any variable with respect to the strain tensor eps.

Note

Keep the order first declare eps, then initialise it and afterwards set it as dofs

eps.set_dofs();

Now we call the templated function via the Sacado data types to get the resulting stress tensor sigma.
To give you an impression of how much longer computations with the Sacado data type take, we also measure the time needed for the computation

timer.enter_subsection("Stress via fad_double");
  SymmetricTensor<2,dim,fad_double> sigma = stress_strain_relation ( eps, kappa, mu );
timer.leave_subsection();
std::cout << "Stress via fad_double:" << extract_value_from_Sacado<dim> (sigma) << std::endl;

Finally we declare our desired tangent as the fourth order tensor C_Sacado and compute the tangent via the command get_tangent.

SymmetricTensor<4,dim> C_Sacado;
eps.get_tangent(C_Sacado, sigma);

For comparsion we can also compute the pure values of the stress tensor by calling the templated function with the normal data type double.

timer.enter_subsection("Stress via double");
  SymmetricTensor<2,dim,double> sigma_d = stress_strain_relation ( eps_d, kappa, mu );
timer.leave_subsection();
std::cout << "Stress via double:    " << sigma_d << std::endl;

As you can see from the times shown in the command window after you ran the code. The computation via the Sacado data types takes here around 4...6 times longer than using the standard type double. However, you have to keep in mind that Sacado computes the tangent whilst computing the stress. Depending on how complicated and computationally demanding the analytical tangent is, Sacado can possibly compete.

Note

This also means that you should only use the Sacado data types when you are actually interested in the derivatives. Else the computation is just too expensive.

}
 
 
/*
 * The main function just calls all the examples and puts some space between the outputs.
 */
int main ()
{
    sacado_test_scalar ();
 
    std::cout << std::endl;
 
    sacado_test_2 ();
 
    std::cout << std::endl;
 
    sacado_test_3 ();
 
    std::cout << std::endl;
 
    sacado_test_3B ();
 
    std::cout << std::endl;
 
    sacado_test_4();
 
    std::cout << std::endl;
 
    sacado_test_5();
 
    std::cout << std::endl;
 
    sacado_test_6();
 
    std::cout << std::endl;
 
    sacado_test_7();
 
    std::cout << std::endl;
 
    sacado_test_8();
 
    std::cout << std::endl;
 
    sacado_test_9();
 
    std::cout << std::endl;
 
    sacado_test_10();
}

The End

Hosted via GitHub according to https://goseeky.wordpress.com/2017/07/22/documentation-101-doxygen-with-github-pages/
Design of the documentation inspired by the deal.ii tutorial programs and created as shown here: https://github.com/jfriedlein/Custom_Doxygen_Documentation