Sacado_example.cc File Reference

#include <deal.II/base/symmetric_tensor.h>
#include <iostream>
#include <fstream>
#include <cmath>
#include <deal.II/base/timer.h>
#include <Sacado.hpp>
#include "Sacado_Wrapper.h"
#include "Sacado-auxiliary_functions.h"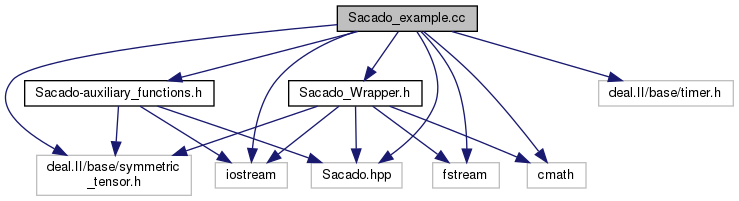

Include dependency graph for Sacado_example.cc:

Typedefs
using	fad_double = Sacado::Fad::DFad< double >

Functions
void	sacado_test_scalar ()
void	sacado_test_2 ()
void	sacado_test_3 ()
void	sacado_test_3B ()
void	sacado_test_4 ()
void	sacado_test_5 ()
void	sacado_test_6 ()
void	sacado_test_7 ()
void	sacado_test_8 ()
void	sacado_test_9 ()
template<int dim, typename Number >
SymmetricTensor< 2, dim, Number >	stress_strain_relation (const SymmetricTensor< 2, dim, Number > &eps, const double &kappa, const double &mu)
void	sacado_test_10 ()
int	main ()

Typedef Documentation

fad_double

using fad_double = Sacado::Fad::DFad<double>

Function Documentation

main()

int main

(

)

References sacado_test_10(), sacado_test_2(), sacado_test_3(), sacado_test_3B(), sacado_test_4(), sacado_test_5(), sacado_test_6(), sacado_test_7(), sacado_test_8(), sacado_test_9(), and sacado_test_scalar().

{
    sacado_test_scalar ();

    std::cout << std::endl;

    sacado_test_2 ();

    std::cout << std::endl;

    sacado_test_3 ();

    std::cout << std::endl;

    sacado_test_3B ();

    std::cout << std::endl;

    sacado_test_4();

    std::cout << std::endl;

    sacado_test_5();

    std::cout << std::endl;

    sacado_test_6();

    std::cout << std::endl;

    sacado_test_7();

    std::cout << std::endl;

    sacado_test_8();

    std::cout << std::endl;

    sacado_test_9();

    std::cout << std::endl;

    sacado_test_10();
}

sacado_test_10()

void sacado_test_10

(

)

References Sacado_Wrapper::SymTensor< dim >::get_tangent(), Sacado_Wrapper::SymTensor< dim >::init(), Sacado_Wrapper::SymTensor< dim >::set_dofs(), and stress_strain_relation().

Referenced by main().

{
    std::cout << "Test 10:" << std::endl;
    const unsigned int dim=3;
    // To measure the computation time of certain sections (see below)
    TimerOutput timer (std::cout, TimerOutput::summary, TimerOutput::cpu_times);

    // The following declarations are usually input arguments. So you receive the strain tensor and the constants out of doubles.
    SymmetricTensor<2,dim> eps_d;
    eps_d[0][0] = 1;
    eps_d[1][1] = 2;
    eps_d[2][2] = 3;

    eps_d[0][1] = 4;
    eps_d[0][2] = 5;
    eps_d[1][2] = 6;

    double kappa = 5;
    double mu = 2;

    // Now we start working with Sacado: \n
    // When we use the index notation to compute e.g. our stress we do not need to declare our constants (here kappa, mu) as
    // fad_double.

    // We declare our strain tensor as the special data type Sacado_Wrapper::SymTensor from the file "Sacado_Wrapper.h"
    // where this data type was derived from the SymmetricTensor<2,dim,fad_double>.
     Sacado_Wrapper::SymTensor<dim> eps;

    // Next we initialize our Sacado strain tensor with the values of the inputed double strain tensor:
     eps.init(eps_d);

    // We define all the entries in the symmetric tensor \a eps as the dofs. So we can later derive any variable
    // with respect to the strain tensor \a eps.
    // @note Keep the order first declare \a eps, then initialise it and afterwards set it as dofs

     eps.set_dofs();

    // Now we call the templated function via the Sacado data types to get the resulting stress tensor \a sigma. \n
    // To give you an impression of how much longer computations with the Sacado data type take,
    // we also measure the time needed for the computation
     timer.enter_subsection("Stress via fad_double");
       SymmetricTensor<2,dim,fad_double> sigma = stress_strain_relation ( eps, kappa, mu );
     timer.leave_subsection();
     std::cout << "Stress via fad_double:" << extract_value_from_Sacado<dim> (sigma) << std::endl;

    // Finally we declare our desired tangent as the fourth order tensor \a C_Sacado and compute the tangent via
    // the command \a get_tangent.
     SymmetricTensor<4,dim> C_Sacado;
     eps.get_tangent(C_Sacado, sigma);

    // For comparsion we can also compute the pure values of the stress tensor by calling
    // the templated function with the normal data type \a double.
     timer.enter_subsection("Stress via double");
       SymmetricTensor<2,dim,double> sigma_d = stress_strain_relation ( eps_d, kappa, mu );
     timer.leave_subsection();
     std::cout << "Stress via double:    " << sigma_d << std::endl;

    // As you can see from the times shown in the command window after you ran the code.
    // The computation via the Sacado data types takes here around 4...6 times longer than
    // using the standard type \a double. However, you have to keep in mind that Sacado
    // computes the tangent whilst computing the stress. Depending on how complicated and computationally demanding the
    // analytical tangent is, Sacado can possibly compete.

    // @note
    // This also means that you should only use the Sacado data types when you are actually
    // interested in the derivatives. Else the computation is just too expensive.

}

sacado_test_2()

void sacado_test_2

(

)

Referenced by main().

{
    std::cout << "Test 2:" << std::endl;

    // First we set the dimension \a dim: 2D->dim=2; 3D->dim=3 \n This defines the "size" of the tensors and the number of dofs. \ref Ex2 "Example 2" only works in 3D, whereas the following Ex3 is set up dimension-independent.
    const unsigned int dim = 3;

    // Declare our input, auxiliary and output variables as SymmetricTensors consisting of fad_doubles (instead of the standard SymmetricTensor out of doubles)
    SymmetricTensor<2,dim, fad_double> sigma, eps;

    // Init the strain tensor (the point at which the derivative shall be computed)
    eps[0][0] = 1;
    eps[1][1] = 2;
    eps[2][2] = 3;
    eps[0][1] = 4;
    eps[0][2] = 5;
    eps[1][2] = 6;

    // Now we declare the dofs. The derivative to a tensor requires all components, therefore we set the components of the strain tensor here one by one as the dofs.
    // Because our tensors are symmetric, we only need 6 components in 3D instead of 9 for a full second order tensor
    eps[0][0].diff(0,6);
    eps[1][1].diff(1,6);
    eps[2][2].diff(2,6);
    eps[0][1].diff(3,6);
    eps[0][2].diff(4,6);
    eps[1][2].diff(5,6);

    // The equation describing the stresses (here just a simple test case)
    sigma = eps;

    // Let's output the computed stress tensor.
    std::cout << sigma << std::endl;
    // The resulting values of \a sigma are fairly boring, due to our simple equation. It is the additional output generated by
    // this, that is interesting here: \n
    // output: \n
    // 1 [ 1 0 0 0 0 0 ] 4 [ 0 0 0 1 0 0 ] 5 [ 0 0 0 0 1 0 ] 4 [ 0 0 0 1 0 0 ] 2 [ 0 1 0 0 0 0 ] 6 [ 0 0 0 0 0 1 ] 5 [ 0 0 0 0 1 0 ] 6 [ 0 0 0 0 0 1 ] 3 [ 0 0 1 0 0 0 ] \n
    // The numbers 1, 4, 5, 4, ... are the entries in the stress tensor \a sigma. In square brackets we see the derivatives of sigma with respect to all the dofs set previously
    // given in the order we defined them above. Meaning: The first entry in the square brackets corresponds to the 0-th dof set by
    // @code eps[0][0].diff(0,6); @endcode referring to the component (0,0) in the strain tensor \a eps.

    // Computing the derivatives for certain components of the resulting tangent modulus: \n
    // We now access these lists of derivatives (output above in square brackets) for one component of the stress tensor \a sigma at a time.
    {
        // Access the derivatives corresponding to the component (0,0) of the stress tensor \a sigma
        double *derivs = &sigma[0][0].fastAccessDx(0);
        // The following output will show us the same derivatives that we already saw above, just formatted differently \n
        // output: d_sigma[0][0]/d_eps = 1 , 0 , 0 , 0 , 0 , 0 ,
        std::cout << "d_sigma[0][0]/d_eps = ";
        for ( unsigned int i=0; i<6; ++i)
            std::cout << derivs[i] << " , ";
        std::cout << std::endl;
    }
    {
        // Access the derivatives corresponding to the component (1,2) of the stress tensor \a sigma
        double *derivs = &sigma[1][2].fastAccessDx(0);
        // output: d_sigma[1][2]/d_eps = 0 , 0 , 0 , 0 , 0 , 1 ,
        std::cout << "d_sigma[1][2]/d_eps = ";
        for ( unsigned int i=0; i<6; ++i)
            std::cout << derivs[i] << " , ";
        std::cout << std::endl;
    }
}

sacado_test_3()

void sacado_test_3

(

)

Referenced by main().

{
    std::cout << "Test 3:" << std::endl;

    const unsigned int dim = 3;

    // Here we also define some constant, for instance the bulk modulus \a kappa and the second Lamè parameter \a mu.
    // We now also define one of our constants as fad_double. By doing this we can use the normal multiplication (see below).
    double kappa_param = 5;
    fad_double kappa (kappa_param);
    // The second constant remains as a double just to show the difference.
    double mu = 2;

    SymmetricTensor<2,dim, fad_double> sigma, eps;

    // To simplify the access to the dofs we define a map that relate the components of our strain tensor to the dof-nbr
    std::map<unsigned int,std::pair<unsigned int,unsigned int>> std_map_indicies;

    // The point at which the derivative shall be computed: \n
    // As mentioned previously, we will implement this example for 2D and 3D, hence we once have to set up a strain tensor
    // and the derivatives for 3D with 6 independent components ...
    if(dim==3)
    {
        eps[0][0] = 1;
        eps[1][1] = 2;
        eps[2][2] = 3;
        
        eps[0][1] = 4;
        eps[0][2] = 5;
        eps[1][2] = 6;
        
        
        eps[0][0].diff(0,6);
        eps[0][1].diff(1,6);
        eps[0][2].diff(2,6);
        eps[1][1].diff(3,6);
        eps[1][2].diff(4,6);
        eps[2][2].diff(5,6);
        
        // By using the map and the following pairs, we have to set up the relation between strain components and dofs only once
        // and can use the map to access the entries of the list later, without possibly mixing up indices and creating errors.
        // Please don't be confused, but the dofs in the Wrapper are set up
        // in a different order that we showed earlier. Earlier: (0,0)-(1,1)-(2,2)-...; Now: (0,0)-(0,1)-(0,2)-...
        std::pair<unsigned int, unsigned int> tmp_pair;
        tmp_pair.first=0; tmp_pair.second=0;
        std_map_indicies[0] = tmp_pair;

        tmp_pair.first=0; tmp_pair.second=1;
        std_map_indicies[1] = tmp_pair;

        tmp_pair.first=0; tmp_pair.second=2;
        std_map_indicies[2] = tmp_pair;

        tmp_pair.first=1; tmp_pair.second=1;
        std_map_indicies[3] = tmp_pair;

        tmp_pair.first=1; tmp_pair.second=2;
        std_map_indicies[4] = tmp_pair;

        tmp_pair.first=2; tmp_pair.second=2;
        std_map_indicies[5] = tmp_pair;
    }
    // ... and once for 2D with just 3 independent components.
    else if(dim==2)
    {
        eps[0][0] = 1;
        eps[1][1] = 2;
        
        eps[0][1] = 4;

                
        eps[0][0].diff(0,3);
        eps[0][1].diff(1,3);
        eps[1][1].diff(2,3);
        
        std::pair<unsigned int, unsigned int> tmp_pair;
        tmp_pair.first=0; tmp_pair.second=0;
        std_map_indicies[0] = tmp_pair;
        
        tmp_pair.first=0; tmp_pair.second=1;
        std_map_indicies[1] = tmp_pair;
        
        tmp_pair.first=1; tmp_pair.second=1;
        std_map_indicies[2] = tmp_pair;        
    }
    else
    {
        throw std::runtime_error("only dim==2 or dim==3 allowed");
    }

    // Instead of calling the *.diff(*) on the components one-by-one we could also use the following for-loop, so
    // we also use the map to set the dofs (as we will do in the Wrapper later).
    // @code
    // for ( unsigned int x=0; x<((dim==2)?3:6); ++x )
    // {
    //  unsigned int i=std_map_indicies[x].first;
    //  unsigned int j=std_map_indicies[x].second;
    //  eps[i][j].diff(x,((dim==2)?3:6));
    // }
    // @endcode

    // For our slightly more complicated stress equation we need the unit and deviatoric tensors.
    // We can simply define them by writing the values of the already existing deal.ii functions into newly
    // defined SymmetricTensors build from fad_doubles.
    SymmetricTensor<2,dim, fad_double> stdTensor_I (( unit_symmetric_tensor<dim,fad_double>()) );
    SymmetricTensor<4,dim, fad_double> stdTensor_Idev ( (deviator_tensor<dim,fad_double>()) );
    
    // With everything set and defined, we can compute our stress \a sigma according to:
    // \f[ \sigma = \kappa \cdot trace(\varepsilon) \cdot \boldsymbol{I} + 2 \cdot \mu \cdot \varepsilon^{dev} \f]
    // Here you can see that we can directly multiply the constant and the tensors when kappa is also declared as fad_double
    sigma = kappa * (trace(eps) *  stdTensor_I);
    // We didn't do the same for mu to once again emphasize the difference between constants as double and as fad_double. \n
    // The remaining code uses a normal double constant.
    SymmetricTensor<2,dim,fad_double> tmp = deviator<dim,fad_double>(symmetrize<dim,fad_double>(eps)); tmp*=(mu*2);
    sigma +=  tmp;
    // The fairly cumbersome computation is caused by the way the operators are set up for tensors out of fad_doubles.
    
    std::cout << "sigma=" << sigma << std::endl;

    // Now we want to actually build our tangent modulus called \a C_Sacado that contains all the derivatives and relates
    // the stress tensor with the strain tensor. \n
    // The fourth-order tensor \a C_Sacado is our final goal, we don't have to compute anything that is related to Sacado with
    // this tensor, so we can finally return to our standard SymmetricTensor out of doubles. The latter is necessary to use
    // the tangent in the actual FE code.
    SymmetricTensor<4,dim> C_Sacado;

    // As in \ref Ex2 "example 2" we access the components of the stress tensor one by one. In order to capture all of them we loop over the
    // components i and j of the stress tensor.
    for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
        {
            double *derivs = &sigma[i][j].fastAccessDx(0); // Access the derivatives of the (i,j)-th component of \a sigma

            // To visually ensure that every stress component has in fact all 6 derivatives for 3D or 3 for 2D, we output the size:
            std::cout<<"size: "<<sigma[i][j].size()<<std::endl;

            // We loop over all the dofs. To be able to use this independent of the chosen dimension \a dim, we use a ternary operator
            // to decide whether we have to loop over 6 derivatives or just 3.
            for(unsigned int x=0;x<((dim==2)?3:6);++x)
            {
                unsigned int k=std_map_indicies[x].first;
                unsigned int l=std_map_indicies[x].second;

                if(k!=l)/*Compare to Voigt notation since only SymmetricTensor instead of Tensor*/
                {
                    C_Sacado[i][j][k][l] = 0.5*derivs[x];
                    C_Sacado[i][j][l][k] = 0.5*derivs[x];
                }
                else
                    C_Sacado[i][j][k][l] = derivs[x];
            }            
            
        }

    // After resembling the fourth-order tensor, we now have got our tangent saved in \a C_Sacado ready to be used

    // To ensure that Sacado works properly, we can compute the analytical tangent for comparison
    double kappa_d = 5;
    double mu_d = 2;
    // Our stress equation in this example is still simple enough to derive the tangent analytically by hand:
    // \f[ \overset{4}{C_{analy}} = \kappa \cdot \boldsymbol{I} \otimes \boldsymbol{I} + 2 \cdot \mu \cdot \overset{4}{I^{dev}} \f]
    SymmetricTensor<4,dim> C_analy = kappa_d * outer_product(unit_symmetric_tensor<dim>(), unit_symmetric_tensor<dim>()) + 2* mu_d * deviator_tensor<dim>();


    // We again define our strain tensor \a eps_d (*_d for standard double in contrast to fad_double)
    SymmetricTensor<2,dim> eps_d;
    
    if(dim==3)
    {
        eps_d[0][0] = 1;
        eps_d[1][1] = 2;
        eps_d[2][2] = 3;
        
        eps_d[0][1] = 4;
        eps_d[0][2] = 5;
        eps_d[2][1] = 6;

    }
    else if(dim==2)
    {
        eps_d[0][0] = 1;
        eps_d[1][1] = 2;
        
        eps_d[1][0] = 4;
        
    }
    else
    {
        throw std::runtime_error("only dim==2 or dim==3 allowed");
    }
    // @todo use boldsymbol for tensors

    // To output the stress tensor we first have to compute it. We do this here via
    // \f[ \sigma = \overset{4}{C_{analy}} : \varepsilon \f]
    // The output exactly matched the result obtained with Sacado.
    // @note Checking the Sacado stress tensor against an analytically computed or otherwise determined stress tensor is absolutely no way to check whether
    // the tangent computed via Sacado is correct. When we compute the stress tensor with Sacado and for example mix up a + and - sign, this might not matter
    // at all if the number that is added or subtracted is small. However, for the tangent this nasty sign can be very critical. Just keep in mind: the
    // tangent has 81 components and the stress tensor just 9, so how does one want to verify 81 variables by comparing 9?

    std::cout << "sigma_analy: " << (C_analy*eps_d) << std::endl;
    
    // That's the reason we compare all the entries in the Sacado and the analytical tensor one by one
    for (unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j)
            for ( unsigned int k=0; k<dim; ++k)
                for ( unsigned int l=0; l<dim; ++l)
                    std::cout << "C_analy["<<i<<"]["<<j<<"]["<<k<<"]["<<l<<"] = " << C_analy[i][j][k][l] << " vs C_Sacado: " << C_Sacado[i][j][k][l] << std::endl;


    // To simplify the comparison we compute a scalar error as the sum of the absolute differences of each component
    double error_Sacado_vs_analy=0;
    for (unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j)
            for ( unsigned int k=0; k<dim; ++k)
                for ( unsigned int l=0; l<dim; ++l)
                    error_Sacado_vs_analy += std::fabs(C_Sacado[i][j][k][l] - C_analy[i][j][k][l]);
                    

    // As desired: The numerical error is zero (0 in double precision) and the tensor components are equal
    std::cout << "numerical error: " << error_Sacado_vs_analy << std::endl;
}

sacado_test_3B()

void sacado_test_3B

(

)

References Sacado_Wrapper::SymTensor< dim >::get_tangent(), Sacado_Wrapper::SymTensor< dim >::init(), and Sacado_Wrapper::SymTensor< dim >::set_dofs().

Referenced by main().

{
    std::cout << "Test 3B:" << std::endl;
    const unsigned int dim=3;

    // The following declarations are usually input arguments. So you receive the strain tensor and the constants out of doubles.
    SymmetricTensor<2,dim> eps_d;
    eps_d[0][0] = 1;
    eps_d[1][1] = 2;
    eps_d[2][2] = 3;

    eps_d[0][1] = 4;
    eps_d[0][2] = 5;
    eps_d[1][2] = 6;

    double kappa = 5;
    double mu = 2;

    // Now we start working with Sacado: \n
    // When we use the index notation to compute e.g. our stress we do not need to declare our constants (here kappa, mu) as
    // fad_double.

    // We declare our strain tensor as the special data type Sacado_Wrapper::SymTensor from the file "Sacado_Wrapper.h"
    // where this data type was derived from the SymmetricTensor<2,dim,fad_double>.
     Sacado_Wrapper::SymTensor<dim> eps;

    // Next we initialize our Sacado strain tensor with the values of the inputed double strain tensor:
     eps.init(eps_d);

    // We define all the entries in the symmetric tensor \a eps as the dofs. So we can later derive any variable
    // with respect to the strain tensor \a eps.
    // @note Keep the order first declare \a eps, then initialise it and afterwards set it as dofs

     eps.set_dofs();

    // Now we declare our output and auxiliary variables as Sacado-Tensors.
     SymmetricTensor<2,dim,fad_double> sigma;

     SymmetricTensor<2,dim, fad_double> stdTensor_I (( unit_symmetric_tensor<dim,fad_double>()) );

     // Our stress equation is now computed in index notation to simplify the use of the constants and
     // especially the use of the \a deviator.
      for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
            sigma[i][j] = kappa * trace(eps) *  stdTensor_I[i][j] + 2. * mu * deviator(eps)[i][j];

    // Finally we declare our desired tangent as the fourth order tensor \a C_Sacado and compute the tangent via
    // the command \a get_tangent.
     SymmetricTensor<4,dim> C_Sacado;
     eps.get_tangent(C_Sacado, sigma);

    // We could again compare the herein computed tangent with the analytical tangent from Ex2, but as before
    // the results are fairly boring, because Sacado hits the analytical tangent exactly --- no surprise for such
    // simple equations.

    // And that's it. By using the Sacado_wrapper we can achieve everything from Ex2 (besides the equations)
    // with just four lines of code namely:
    // - eps.init(eps_d);    // To initialize the Sacado strain tensor
    // - eps.set_dofs();     // To declare the components of eps as the dofs
    // - eps.get_tangent(*); // To get the tangent
}

sacado_test_4()

void sacado_test_4

(

)

References Sacado_Wrapper::SymTensor< dim >::get_tangent(), Sacado_Wrapper::SW_double< dim >::get_tangent(), Sacado_Wrapper::SymTensor< dim >::init(), Sacado_Wrapper::SW_double< dim >::init(), and Sacado_Wrapper::DoFs_summary< dim >::set_dofs().

Referenced by main().

{
    std::cout << "Test 4:" << std::endl;
    const unsigned int dim=3;

    // The following declarations are usually input arguments. So you receive the strain tensor \q eps_d,
    // the damage variable \a phi and the constants \a kappa and \a mu out of doubles.
    SymmetricTensor<2,dim> eps_d;
    eps_d[0][0] = 1;
    eps_d[1][1] = 2;
    eps_d[2][2] = 3;

    eps_d[0][1] = 4;
    eps_d[0][2] = 5;
    eps_d[1][2] = 6;

    double phi_d = 0.3;

    // We don't need these constants in the current example.
    // double kappa = 5;
    // double mu = 2;


    // We set up our strain tensor as in Ex3B.
     Sacado_Wrapper::SymTensor<dim> eps;
     Sacado_Wrapper::SW_double<dim> phi;

    // Initialize the strain tensor and the damage variable
     eps.init(eps_d);
     phi.init(phi_d);

     // Set the dofs, where the argument sets the total nbr of dofs (3 or 6 for the sym. tensor and 1 for the double)
//    eps.set_dofs(eps.n_independent_components+1/*an additional dof for phi*/);
//
     // In order to also compute derivatives with respect to the scalar \a phi, we add this scalar to our list
     // of derivatives. Because we have already defined 3 or 6 dofs our additional dof will be placed at the end
     // of this list. We set this up with the member variable start_index ...
//    phi.start_index=eps.n_independent_components;
     // and again using the input argument representing the total number of dofs
//    phi.set_dofs(eps.n_independent_components+1);

    // All of the above 3 lines of code are automatically done by the DoFs_summary class. So, to
    // set our dofs we just create an instance and call set_dofs with our variables containing the desired dofs.
     Sacado_Wrapper::DoFs_summary<dim> DoFs_summary;
     DoFs_summary.set_dofs(eps, phi);


    // Compute the stress tensor and damage variable \a d (here we just use some arbitrary equations for testing): \n
     // Let us first declare our output (and auxiliary) variables as Sacado data types.
      SymmetricTensor<2,dim,fad_double> sigma;
      fad_double d;
     // @todo It would be nice to use the data types from the Sacado_Wrapper for all the Sacado variables. But
     // somehow the operators (multiply*, ...) seem to cause conflicts again.

     // The actual computation in the following scope uses the exact same equation as your normal computation e. g. via the data type double.
     // Hence, you could either directly compute your stress, etc. via the Sacado variables or you define
     // template functions that contain your equations and are either called templated with double or fad_double.
     // When using the first option, please consider the computation time that is generally higher for a computation
     // with fad_double than with normal doubles (own experience in a special case: slower by factor 30).
     // The second option with templates does not suffer these issues.
      {
      d = phi*phi + 25 + trace(eps) + eps.norm();
      std::cout << "d=" << d << std::endl;

      for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
            sigma[i][j] = phi * d * eps[i][j];
             // ToDo: strangely when phi is a fad_double then the multiplication phi * eps works directly without
             // having to use the index notation
      std::cout << "sigma=" << sigma << std::endl << std::endl;
      }


    // Get the tangents
     // d_sigma / d_eps: SymmetricTensor with respect to SymmetricTensor
      SymmetricTensor<4,dim> C_Sacado;
      eps.get_tangent(C_Sacado, sigma);
      std::cout << "C_Sacado=" << C_Sacado << std::endl;

     // Compute the analytical tangent:
      SymmetricTensor<4,dim> C_analy;
      C_analy = ( std::pow(phi_d, 3) + 25*phi_d + phi_d*trace(eps_d) + phi_d*eps_d.norm() ) * identity_tensor<dim>()
                + phi_d * outer_product( eps_d, unit_symmetric_tensor<dim>())
                + phi_d * outer_product( eps_d, eps_d ) * 1./eps_d.norm();
      // @note Be aware of the difference between \f[ eps_d \otimes \boldsymbol{1} \text{ and } \boldsymbol{1} \otimes eps_d \f]

      std::cout << "C_analy =" << C_analy << std::endl;

      // To simplify the comparison we compute a scalar error as the sum of the absolute differences of each component
       double error_Sacado_vs_analy=0;
       for (unsigned int i=0; i<dim; ++i)
            for ( unsigned int j=0; j<dim; ++j)
                for ( unsigned int k=0; k<dim; ++k)
                    for ( unsigned int l=0; l<dim; ++l)
                        error_Sacado_vs_analy += std::fabs(C_Sacado[i][j][k][l] - C_analy[i][j][k][l]);
       std::cout << "numerical error: " << error_Sacado_vs_analy << std::endl << std::endl;

     // d_d / d_eps: double with respect to SymmetricTensor
      SymmetricTensor<2,dim> d_d_d_eps;
      eps.get_tangent(d_d_d_eps, d);
      std::cout << "d_d_d_eps      =" << d_d_d_eps << std::endl;
      SymmetricTensor<2,dim> d_d_d_eps_analy;
      d_d_d_eps_analy = unit_symmetric_tensor<dim>() + eps_d / eps_d.norm();
      std::cout << "d_d_d_eps_analy=" << d_d_d_eps_analy << std::endl << std::endl;

     // d_sigma / d_phi: SymmetricTensor with respect to double
      SymmetricTensor<2,dim> d_sigma_d_phi;
      phi.get_tangent(d_sigma_d_phi, sigma);
      std::cout << "d_sigma_d_phi      =" << d_sigma_d_phi << std::endl;
      SymmetricTensor<2,dim> d_sigma_d_phi_analy;
      d_sigma_d_phi_analy = ( phi_d*phi_d + 25 + trace(eps_d) + eps_d.norm() + 2 * phi_d*phi_d ) * eps_d;
      std::cout << "d_sigma_d_phi_analy=" << d_sigma_d_phi_analy << std::endl << std::endl;

     // Retrieve the values stored in \a sigma:
      SymmetricTensor<2,dim> sigma_d;
      for ( unsigned int i=0; i<dim; ++i)
            for ( unsigned int j=0; j<dim; ++j )
                sigma_d[i][j] = sigma[i][j].val();
      std::cout << "sigma_d = " << sigma_d << std::endl;

     // d_d / d_phi: double with respect to double
      double d_d_d_phi;
      phi.get_tangent(d_d_d_phi, d);
      std::cout << "d_d_d_phi=" << d_d_d_phi << std::endl;

     // Retrieve the value stored in d
      double d_double = d.val();

     // Taylor-series for point x
     // @todo Maybe add some more text on the linearization
      double x = phi_d + 0.05;
      std::cout << "d_lin = d_d_d_phi * (phi_d - x) + d@(phi_d) = " << d_d_d_phi * (x-phi_d) + d_double << std::endl;
      std::cout << "d@x = " << x*x + 25 + trace(eps_d) + eps_d.norm() << std::endl;

    // And that's it. By using the Sacado_wrapper we can compute derivatives with respect to
    // a tensor and a scalar at the same time (besides the equations)
    // in essence with just the following lines of code namely:
    // - eps.init(eps_d); phi.init(phi_d);   // To initialize the Sacado strain tensor and scalar damage variable
    // - DoFs_summary.set_dofs(eps, phi);    // To declare the components of eps and phi as the dofs
    // - eps.get_tangent(*); // To get tangents with respect to eps
    // - phi.get_tangent(*); // To get tangents with respect to phi
}

sacado_test_5()

void sacado_test_5

(

)

Referenced by main().

{
    const unsigned int dim=3;
    std::cout << "Test 5:" << std::endl;
    Tensor<1,dim,fad_double> c;
    fad_double a,b;
    unsigned int n_dofs=2;
    a = 1; b = 2;   // at the point (a,b) = (1,2)
    a.diff(0,2);  // Set a to be dof 0, in a 2-dof system.
    b.diff(1,2);  // Set b to be dof 1, in a 2-dof system.
    // c is now a vector with three components
    c[0] = 2*a+3*b;
    c[1] = 4*a+5*b;
    c[2] = 6*a+7*b;
    
    // Access to the derivatives works as before.
    for(unsigned int i=0;i<dim;++i)
    {
        const fad_double &derivs = c[i]; // Access derivatives
        for(unsigned int j=0;j<n_dofs;++j)
        {
            std::cout << "Derivatives at the point (" << a << "," << b << ") for "
            <<i<<"th component wrt "<<j<<"th direction "<< std::endl;
            std::cout << "dc_i/dxj = " << derivs.fastAccessDx(j) << std::endl;            
        }
    }
}

sacado_test_6()

void sacado_test_6

(

)

Referenced by main().

{
    std::cout << "Test 6:" << std::endl;
    // Define the variables used in the computation (inputs: a, b; output: c; auxiliaries: *) as doubles
     double a=1;
     double b=2;

    // Number of independent variables (scalar a and b)
     int num_dofs = 2;

    // Define another data type containing even more Sacado data types
    // @todo try to merge the fad_double data type with this templated data type
     typedef Sacado::Fad::DFad<double> DFadType;
     Sacado::Fad::DFad<DFadType> afad(num_dofs, 0, a);
     Sacado::Fad::DFad<DFadType> bfad(num_dofs, 1, b);
     Sacado::Fad::DFad<DFadType> cfad;

    // Output the variables: We se that the values of \a a and \a b are set but the derivatives have not yet been fully declared
     std::cout << "afad=" << afad << std::endl;
     std::cout << "bfad=" << bfad << std::endl;
     std::cout << "cfad=" << cfad << std::endl;

    // Now we set the "inner" derivatives.
    afad.val() = fad_double(num_dofs, 0, a); // set afad.val() as the first dof and init it with the double a
    bfad.val() = fad_double(num_dofs, 1, b);

    // Compute function and derivative with AD
     cfad = 2*afad + std::cos(afad*bfad);

    // After this, we output the variables again and see that some additional derivatives have been declared. Furthermore,
    // \a cfad is filled with the values and derivatives
     std::cout << "afad=" << afad << std::endl;
     std::cout << "bfad=" << bfad << std::endl;
     std::cout << "cfad=" << cfad << std::endl;

    // Extract value and derivatives
     double c_ad = cfad.val().val();       // r
     double dcda_ad = cfad.dx(0).val();    // dr/da
     double dcdb_ad = cfad.dx(1).val();    // dr/db
     double d2cda2_ad = cfad.dx(0).dx(0);  // d^2r/da^2
     double d2cdadb_ad = cfad.dx(0).dx(1); // d^2r/dadb
     double d2cdbda_ad = cfad.dx(1).dx(0); // d^2r/dbda
     double d2cdb2_ad = cfad.dx(1).dx(1);  // d^2/db^2

    // Now we can print the actual double value of c and some of the derivatives:
     std::cout << "c_ad=" << c_ad << std::endl;
     std::cout << "Derivatives at the point (" << a << "," << b << ")" << std::endl;
     std::cout << "dc/da = " << dcda_ad << ", dc/db=" << dcdb_ad << std::endl;
     std::cout << "d²c/da² = " << d2cda2_ad << ", d²c/db²=" << d2cdb2_ad << std::endl;
     std::cout << "d²c/dadb = " << d2cdadb_ad << ", d²c/dbda=" << d2cdbda_ad << std::endl;
}

sacado_test_7()

void sacado_test_7

(

)

Referenced by main().

{
    const unsigned int dim=3;

    std::cout << "Test 7:" << std::endl;

    // Defining the inputs (material parameters, strain tensor)
     double lambda=1;
     double mu=2;
     SymmetricTensor<2,dim, double> eps;

     eps[0][0] = 1.;
     eps[1][1] = 2.;
     eps[2][2] = 3.;

     eps[0][1] = 4.;
     eps[0][2] = 5.;
     eps[1][2] = 6.;

    // Here we skip the one-field example and right away show the equations for a two-field problem
    // with \a eps and \a phi.
     double phi=0.3;

    // Setup of the map relating the indices (as before)
     std::map<unsigned int,std::pair<unsigned int,unsigned int>> std_map_indicies;

     std::pair<unsigned int, unsigned int> tmp_pair;
     tmp_pair.first=0; tmp_pair.second=0;
     std_map_indicies[0] = tmp_pair;

     tmp_pair.first=0; tmp_pair.second=1;
     std_map_indicies[1] = tmp_pair;

     tmp_pair.first=0; tmp_pair.second=2;
     std_map_indicies[2] = tmp_pair;

     tmp_pair.first=1; tmp_pair.second=1;
     std_map_indicies[3] = tmp_pair;

     tmp_pair.first=1; tmp_pair.second=2;
     std_map_indicies[4] = tmp_pair;

     tmp_pair.first=2; tmp_pair.second=2;
     std_map_indicies[5] = tmp_pair;

    // Number of independent variables (6 for the tensor and 1 for the scalar phi)
     const unsigned int nbr_dofs = 6+1;

    // Declaring the special data types containing all derivatives
     typedef Sacado::Fad::DFad<double> DFadType;
     SymmetricTensor<2,dim, Sacado::Fad::DFad<DFadType> > eps_fad, eps_fad_squared;
     Sacado::Fad::DFad<DFadType> phi_fad;


    // Setting the dofs
     for ( unsigned int x=0; x<6; ++x )
     {
        unsigned int i=std_map_indicies[x].first;
        unsigned int j=std_map_indicies[x].second;
        (eps_fad[i][j]).diff( x, nbr_dofs); // set up the "inner" derivatives
        (eps_fad[i][j]).val() = fad_double(nbr_dofs, x, eps[i][j]); // set up the "outer" derivatives
     }

     phi_fad.diff( 6, nbr_dofs );
     phi_fad.val() = fad_double(nbr_dofs, 6, phi); // set up the "outer" derivatives

     std::cout << "eps_fad=" << eps_fad << std::endl;
     std::cout << "phi_fad=" << phi_fad << std::endl;

    // Compute eps² = eps_ij * eps_jk in index notation
     for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int k=0; k<dim; ++k )
            for ( unsigned int j=0; j<dim; ++j )
                if ( i>=k )
                    eps_fad_squared[i][k] += eps_fad[i][j] * eps_fad[j][k];

    // Compute the strain energy density
     Sacado::Fad::DFad<DFadType> energy;
     energy = lambda/2. * trace(eps_fad)*trace(eps_fad) + mu * trace(eps_fad_squared) + 25 * phi_fad * trace(eps_fad);

    // Give some insight into the storage of the values and derivatives
     std::cout << "energy=" << energy << std::endl;

    // Compute sigma as \f[ \frac{\partial \Psi}{\partial \boldsymbol{\varepsilon}} \f]
     SymmetricTensor<2,dim> sigma_Sac;
     for ( unsigned int x=0; x<6; ++x )
     {
        unsigned int i=std_map_indicies[x].first;
        unsigned int j=std_map_indicies[x].second;
        if ( i!=j )
            sigma_Sac[i][j] = 0.5 * energy.dx(x).val();
        else
            sigma_Sac[i][j] = energy.dx(x).val();
     }
     std::cout << "sigma_Sacado=" << sigma_Sac << std::endl;

     double d_energy_d_phi = energy.dx(6).val();
     std::cout << "d_energy_d_phi=" << d_energy_d_phi << std::endl;

     double d2_energy_d_phi_2 = energy.dx(6).dx(6);
     std::cout << "d2_energy_d_phi_2=" << d2_energy_d_phi_2 << std::endl;

    // Analytical stress tensor:
     SymmetricTensor<2,dim> sigma;
     sigma = lambda*trace(eps)*unit_symmetric_tensor<dim>() + 2. * mu * eps + 25 * phi * unit_symmetric_tensor<dim>();
     std::cout << "analy. sigma=" << sigma << std::endl;


    // Sacado-Tangent
     SymmetricTensor<4,dim> C_Sac;
     for(unsigned int x=0;x<6;++x)
        for(unsigned int y=0;y<6;++y)
        {
            const unsigned int i=std_map_indicies[y].first;
            const unsigned int j=std_map_indicies[y].second;
            const unsigned int k=std_map_indicies[x].first;
            const unsigned int l=std_map_indicies[x].second;

            double deriv = energy.dx(x).dx(y); // Access the derivatives of the (i,j)-th component of \a sigma

            if ( k!=l && i!=j )
                C_Sac[i][j][k][l] = 0.25* deriv;
            else if(k!=l)/*Compare to Voigt notation since only SymmetricTensor instead of Tensor*/
            {
                C_Sac[i][j][k][l] = 0.5*deriv;
                C_Sac[i][j][l][k] = 0.5*deriv;
            }
            else
                C_Sac[i][j][k][l] = deriv;
        }

    // Analytical tangent
     SymmetricTensor<4,dim> C_analy;
     C_analy = lambda * outer_product(unit_symmetric_tensor<dim>(), unit_symmetric_tensor<dim>()) + 2. * mu * identity_tensor<dim>();

    double error_Sacado_vs_analy=0;
    for (unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j)
            for ( unsigned int k=0; k<dim; ++k)
                for ( unsigned int l=0; l<dim; ++l)
                    error_Sacado_vs_analy += std::fabs(C_Sac[i][j][k][l] - C_analy[i][j][k][l]);

    std::cout << "Numerical error=" << error_Sacado_vs_analy << std::endl;
}

sacado_test_8()

void sacado_test_8

(

)

References Sacado_Wrapper::SW_double2< dim >::get_curvature(), Sacado_Wrapper::DoFs_summary< dim >::get_curvature(), Sacado_Wrapper::SW_double2< dim >::get_tangent(), and Sacado_Wrapper::DoFs_summary< dim >::init_set_dofs().

Referenced by main().

{
    const unsigned int dim=3;

    std::cout << "Test 8:" << std::endl;

    // Defining the inputs (material parameters, strain tensor)
     double lambda=1;
     double mu=2;
     SymmetricTensor<2,dim, double> eps;
     double phi = 0.3;

     eps[0][0] = 1.;
     eps[1][1] = 2.;
     eps[2][2] = 3.;

     eps[0][1] = 4.;
     eps[0][2] = 5.;
     eps[1][2] = 6.;

    // Declaring the special data types containing all derivatives
     typedef Sacado::Fad::DFad<double> DFadType;

    // Declare the variables \a eps_fad and \a phi_fad as the special Wrapper data types
     Sacado_Wrapper::SymTensor2<dim> eps_fad;
     Sacado_Wrapper::SW_double2<dim> phi_fad;

    // Declare the summary data type relating all the dofs and initialising them too
     Sacado_Wrapper::DoFs_summary<dim> DoFs_summary;
     DoFs_summary.init_set_dofs(eps_fad, eps, phi_fad, phi);

    // The variables are outputted to give some insight into the storage of the values (derivatives still trivial).
     std::cout << "eps_fad=" << eps_fad << std::endl;
     std::cout << "phi_fad=" << phi_fad << std::endl;

    // Compute eps² = eps_ij * eps_jk in index notation
     SymmetricTensor<2,dim, Sacado::Fad::DFad<DFadType> > eps_fad_squared;
     for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int k=0; k<dim; ++k )
            for ( unsigned int j=0; j<dim; ++j )
                if ( i>=k )
                    eps_fad_squared[i][k] += eps_fad[i][j] * eps_fad[j][k];

    // Compute the strain energy density
     Sacado::Fad::DFad<DFadType> energy;
     energy = lambda/2. * trace(eps_fad)*trace(eps_fad) + mu * trace(eps_fad_squared) + 25 * phi_fad * trace(eps_fad);

    // The energy is outputted (formatted by hand) to give some insight into the storage of the values and derivatives. \n
    // energy=399 [ 17.5 32 40 21.5 48 25.5 150 ] \n
    // [ 17.5 [ 5 0 0 1 0 1 25 ] 32 [ 0 8 0 0 0 0 0 ] 40 [ 0 0 8 0 0 0 0 ] \n
    // 21.5 [ 1 0 0 5 0 1 25 ] 48 [ 0 0 0 0 8 0 0 ] 25.5 [ 1 0 0 1 0 5 25 ] \n
    // 150 [ 25 0 0 25 0 25 0 ] ]

     std::cout << "energy=" << energy << std::endl;

    // Compute sigma as \f[ \boldsymbol{\sigma} = \frac{\partial \Psi}{\partial \boldsymbol{\varepsilon}} \f]
     SymmetricTensor<2,dim> sigma_Sac;
     eps_fad.get_tangent(sigma_Sac, energy);
     std::cout << "sigma_Sacado=" << sigma_Sac << std::endl;

     double d_energy_d_phi;
     phi_fad.get_tangent(d_energy_d_phi, energy);
     std::cout << "d_energy_d_phi=" << d_energy_d_phi << std::endl;


    // Analytical stress tensor:
     SymmetricTensor<2,dim> sigma;
     sigma = lambda*trace(eps)*unit_symmetric_tensor<dim>() + 2. * mu * eps + 25 * phi * unit_symmetric_tensor<dim>();
     std::cout << "analy. sigma=" << sigma << std::endl;


    // Sacado stress tangent (or eps curvature) as \f[ \frac{\partial^2 \Psi}{\partial \boldsymbol{\varepsilon}^2} \f]
     SymmetricTensor<4,dim> C_Sac;
     eps_fad.get_curvature(C_Sac, energy);

    // Sacado phi curvature as \f[ \frac{\partial^2 \Psi}{\partial \varphi^2} \f]
     double d2_energy_d_phi_2;
     phi_fad.get_curvature(d2_energy_d_phi_2, energy);
     std::cout << "d2_energy_d_phi_2=" << d2_energy_d_phi_2 << std::endl;

    // Sacado derivatives \f[ \frac{\partial^2 \Psi}{\partial \boldsymbol{\varepsilon} \partial \varphi} \f]
     SymmetricTensor<2,dim> d2_energy_d_eps_d_phi;
     DoFs_summary.get_curvature(d2_energy_d_eps_d_phi, energy, eps_fad, phi_fad);
     std::cout << "d2_energy_d_eps_d_phi=" << d2_energy_d_eps_d_phi << std::endl;

    // Sacado derivatives \f[ \frac{\partial^2 \Psi}{\partial \varphi \partial \boldsymbol{\varepsilon}} \f]
     SymmetricTensor<2,dim> d2_energy_d_phi_d_eps;
     DoFs_summary.get_curvature(d2_energy_d_phi_d_eps, energy, phi_fad, eps_fad);
     std::cout << "d2_energy_d_phi_d_eps=" << d2_energy_d_phi_d_eps << std::endl;

    // When you consider the output: \n
    // d2_energy_d_eps_d_phi=25 0 0 0 25 0 0 0 25 \n
    // d2_energy_d_phi_d_eps=25 0 0 0 25 0 0 0 25 \n
    // in detail you will notice that both second derivatives are identical. This compplies with the Schwarz integrability condition (Symmetry of second derivatives)
    // (ignoring all limitation and requirements), it holds
    // \f[ \frac{\partial^2 \Psi}{\partial \boldsymbol{\varepsilon} \partial \varphi} = \frac{\partial^2 \Psi}{\partial \varphi \partial \boldsymbol{\varepsilon}}  \f]

    // Analytical stress tangent
     SymmetricTensor<4,dim> C_analy;
     C_analy = lambda * outer_product(unit_symmetric_tensor<dim>(), unit_symmetric_tensor<dim>()) + 2. * mu * identity_tensor<dim>();

    // Compute the error for the stress tangent
     double error_Sacado_vs_analy=0;
     for (unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j)
            for ( unsigned int k=0; k<dim; ++k)
                for ( unsigned int l=0; l<dim; ++l)
                    error_Sacado_vs_analy += std::fabs(C_Sac[i][j][k][l] - C_analy[i][j][k][l]);
     std::cout << "Numerical error=" << error_Sacado_vs_analy << std::endl;
}

sacado_test_9()

void sacado_test_9

(

)

Referenced by main().

{
    const unsigned int dim=3;

    std::cout << "Test 9:" << std::endl;

    double kappa_param = 5;
    fad_double kappa (kappa_param);
    double mu = 2;

    SymmetricTensor<2,dim, fad_double> sigma, eps;

    std::map<unsigned int,std::pair<unsigned int,unsigned int>> std_map_indicies;

        eps[0][0] = 1;
        eps[1][1] = 2;
        eps[2][2] = 3;

        eps[0][1] = 4;
        eps[0][2] = 5;
        eps[1][2] = 6;


        eps[0][0].diff(0,6);
        eps[0][1].diff(1,6);
        eps[0][2].diff(2,6);
        eps[1][1].diff(3,6);
        eps[1][2].diff(4,6);
        eps[2][2].diff(5,6);

        std::pair<unsigned int, unsigned int> tmp_pair;
        tmp_pair.first=0; tmp_pair.second=0;
        std_map_indicies[0] = tmp_pair;

        tmp_pair.first=0; tmp_pair.second=1;
        std_map_indicies[1] = tmp_pair;

        tmp_pair.first=0; tmp_pair.second=2;
        std_map_indicies[2] = tmp_pair;

        tmp_pair.first=1; tmp_pair.second=1;
        std_map_indicies[3] = tmp_pair;

        tmp_pair.first=1; tmp_pair.second=2;
        std_map_indicies[4] = tmp_pair;

        tmp_pair.first=2; tmp_pair.second=2;
        std_map_indicies[5] = tmp_pair;

    SymmetricTensor<2,dim, fad_double> stdTensor_I (( unit_symmetric_tensor<dim,fad_double>()) );

    sigma = kappa * (trace(eps) *  stdTensor_I);
    SymmetricTensor<2,dim,fad_double> tmp = deviator<dim,fad_double>(symmetrize<dim,fad_double>(eps)); tmp*=(mu*2);
    sigma +=  tmp;

    std::cout << "sigma=" << sigma << std::endl;

     // Retrieve the values stored in \a sigma:
      SymmetricTensor<2,dim> sigma_d;
      for ( unsigned int i=0; i<dim; ++i)
            for ( unsigned int j=0; j<dim; ++j )
                sigma_d[i][j] = sigma[i][j].val();

    SymmetricTensor<4,dim> C_Sacado;

    for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
        {
            double *derivs = &sigma[i][j].fastAccessDx(0); // Access the derivatives of the (i,j)-th component of \a sigma

            for(unsigned int x=0;x<((dim==2)?3:6);++x)
            {
                unsigned int k=std_map_indicies[x].first;
                unsigned int l=std_map_indicies[x].second;

                if(k!=l)/*Compare to Voigt notation since only SymmetricTensor instead of Tensor*/
                {
                    C_Sacado[i][j][k][l] = 0.5*derivs[x];
                    C_Sacado[i][j][l][k] = 0.5*derivs[x];
                }
                else
                    C_Sacado[i][j][k][l] = derivs[x];
            }
        }

    SymmetricTensor<2,dim> eps_d;
    eps_d[0][0] = 1;
    eps_d[1][1] = 2;
    eps_d[2][2] = 3;

    eps_d[0][1] = 4;
    eps_d[0][2] = 5;
    eps_d[1][2] = 6;

    SymmetricTensor<2,dim> stress_from_tangent = C_Sacado*eps_d;

    std::cout << "C_Sacado*eps_d=" << stress_from_tangent << std::endl;
    std::cout << "sigma=         " << sigma_d << std::endl;

    // @todo Add the link to the ac.nz site

    // As you can see we obtain the correct stress tensor only by using the factor 0.5 onto the off-diagonal elements of the symmetric tensor. \n
    // @note So, why do we need the factor 0.5 then? (based on [homepages.engineering.auckland.ac.nz ...])\n
    // When using symmetric tensor one has to be aware of the definition of the independent variables. In 3d those are the
    // following 6 components: \n
    // - \f$ A_{11} \f$
    // - \f$ A_{22} \f$
    // - \f$ A_{33} \f$
    // - \f$ \overline{A_{12}} \f$
    // - \f$ \overline{A_{13}} \f$
    // - \f$ \overline{A_{23}} \f$ \n
    // Here the overlined components denote the averaged values, such that
    // - \f$ \overline{A_{12}} = 0.5 \cdot [ A_{12} + A_{21} ] = A_{12} = A_{21} \f$
    // - ... \n
    // This looks rather boring, because the averaged value of the two identical components (symmetry) is identical to the components.
    // But (and that is a crucial BUT), this only holds for the values NOT the derivatives.
    // The derivative of a function \f$ \Phi \f$ with respect to a symmetric tensor \a A is
    // \f[ \frac{\partial \Phi}{\partial \overline{A_{12}}} = \frac{\partial \Phi}{\partial A_{12}} \cdot \frac{\partial A_{12}}{\partial \overline{A_{12}}}
    //                                                          + \frac{\partial \Phi}{\partial A_{21}} \cdot \frac{\partial A_{21}}{\partial \overline{A_{21}}}
    //                                                          = \frac{\partial \Phi}{\partial A_{12}} + \frac{\partial \Phi}{\partial A_{21}}
    //                                                          = 2 \cdot \frac{\partial \Phi}{\partial A_{12}} \f]
    // Note how the derivatives with respect to the actual tensor components (here 12 and 21) are identical. \n
    // However, our derivatives (computed via Sacado) were calculated with respect to the actually independent
    // variables (overlined). Still, in the tensor with the derivatives we want the derivatives with respect to the normal components (not overlined). \n
    // Summary: \n
    // When you compute derivatives with respect to a symmetric tensor, you have to scale the off-diagonal elements by 0.5 to account for the fact that you actually work with
    // the averaged values. \n
    // As a consequence, we use the factor 0.5 for all off-diagonal components of derivatives with respect to symmetric tensors. For second derivatives with respect to
    // symmetric tensors the factors 0.5 and 0.25 come into play.

}

sacado_test_scalar()

void sacado_test_scalar

(

)

Referenced by main().

{
    std::cout << "Scalar Test:" << std::endl;
    // Define the variables used in the computation (inputs/independent variables: a, b; output/result: c; auxiliaries/passive variables: *) as the Sacado-data type
     fad_double a,b,c;
    // Initialize the input variables a and b; This (a,b) = (1,2) will be the point where the derivatives are computed.
    // Compare: y=x² -> (dy/dx)(\@x=1) = 2. We can only compute the derivative numerically at a certain point.
     a = 1;
     b = 2;

    a.diff(0,2);  // Set a to be dof 0, in a 2-dof system.
    b.diff(1,2);  // Set b to be dof 1, in a 2-dof system.
    // Our equation here is very simply. But you can use nested equations and many standard mathematical operations, such as sqrt, pow, sin, ...
    c = 2*a + std::cos(a*b);
    double *derivs = &c.fastAccessDx(0); // Access the derivatives of
    // Output the derivatives of c with respect to the two above defined degrees of freedom (dof)
    std::cout << "Derivatives at the point (" << a << "," << b << ")" << std::endl;
    std::cout << "dc/da = " << derivs[0] << ", dc/db=" << derivs[1] << std::endl;
}

stress_strain_relation()

template<int dim, typename Number >

SymmetricTensor<2,dim,Number> stress_strain_relation	(	const SymmetricTensor< 2, dim, Number > &	eps,
		const double &	kappa,
		const double &	mu
	)

Referenced by sacado_test_10().

{
    SymmetricTensor<2,dim,Number> sigma;

    SymmetricTensor<2,dim,Number> stdTensor_I (( unit_symmetric_tensor<dim,Number>()) );

    // Our stress equation is now computed in index notation to simplify the use of the constants and
    // especially the use of the \a deviator.
     for ( unsigned int i=0; i<dim; ++i)
        for ( unsigned int j=0; j<dim; ++j )
            sigma[i][j] = kappa * trace(eps) *  stdTensor_I[i][j] + 2. * mu * deviator(eps)[i][j];

    return sigma;
}